Jekyll Blog와 MathJax

Jekyll Blog

깃허브 블로그는 github_id.github.io 형식의 URL을 가진 블로그를 만들 수 있습니다.
블로그 URL을 자신의 깃허브에 repository로 생성하면 자동으로 contributors에 github-actions[bot]이 추가되고 Environments에 github-pages가 세팅이 됩니다.

깃허브 블로그는 Jekyll이라는 템플릿, 인라인 코드, 마크다운 같은 동적 요소들을 정적인 웹페이지로 구성해주는 파싱 엔진입니다.
직접 Jekyll Theme을 구성하고 제작하는 것도 좋지만 기본적으로 만들어진 템플릿 요소를 직접 커스터마이징 하는 것을 추천합니다.
솔직히 말해서 직접 만드는 것은 신경써야 할 요소가 너무 많기도 하고 이 Jekyll이라 녀석이 liquid라는 언어를 활용하기 때문에 여러모로 번거로운 작업이 많아집니다.
설치 방법은 검색하면 저보다 잘 알려주는 글이 많기 때문에 저는 지킬 블로그 커스터마이징 위주로 설명하겠습니다.

Jekyll Blog 테마 선택 Tip

‘Jekyll Blog 테마 추천’ 이런 검색어를 검색하면 맘에 드는 테마가 생각보다 많지 않을 것입니다. 이럴때 제가 대체적으로 많이 쓰는 방법은 여러 블로그를 돌아다니다가 맘에 드는 테마를 발견하면 그 블로그의 원본 테마링크를 타고 가거나 해당 블로그를 clone으로 다운받고 re cumtomizing을 하기도 합니다.

대체로 해당 블로그 하단부에 테마의 원본 링크가 있습니다.

지금 제가 사용중인 테마는 Chirpy 테마인데 이 테마는 기존 지킬과 다르게 테마 적용에 상당히 난이도가 높았기때문에 지킬 블로그 구성이 익숙치 않으신 분에게는 추천드리지 않습니다.
초보 지킬 블로거에게 추천하는 테마는 Minimal Mistakes 기반의 테마입니다. 해당 검색어로 검색하면 세팅을 말하면서 Minimal Mistake 테마로 구성된 블로그들을 볼 수 있습니다. 참고하시면 될 것 같습니다.

Jekyll Blog Customizing Tip

제 블로그의 구성 폴더입니다.

지킬블로그는 Rudy를 기반으로 설치와 빌드를 하는 경우가 많기 때문에 .gem이나 .gemspec 파일이 동봉된 경우가 많습니다.
블로그의 구성 중 가장 중요한 파일은 _config.yml입니다.
이 파일은 전체 블로그의 세팅을 처리하는 부분이 담겨있습니다. 또한 이 부분이 중요한 이유는 앞서 언급한 liquid의 특성 때문입니다.
최근의 웹페이지 구성은 head단, body단을 한 파일에 모두 넣는 방식이 아닌 분리해서 레고처럼 조립하는 방식을 선호하는 것 같습니다. 지킬 블로그 제작도 보통 동일한 방식으로 구성됩니다.

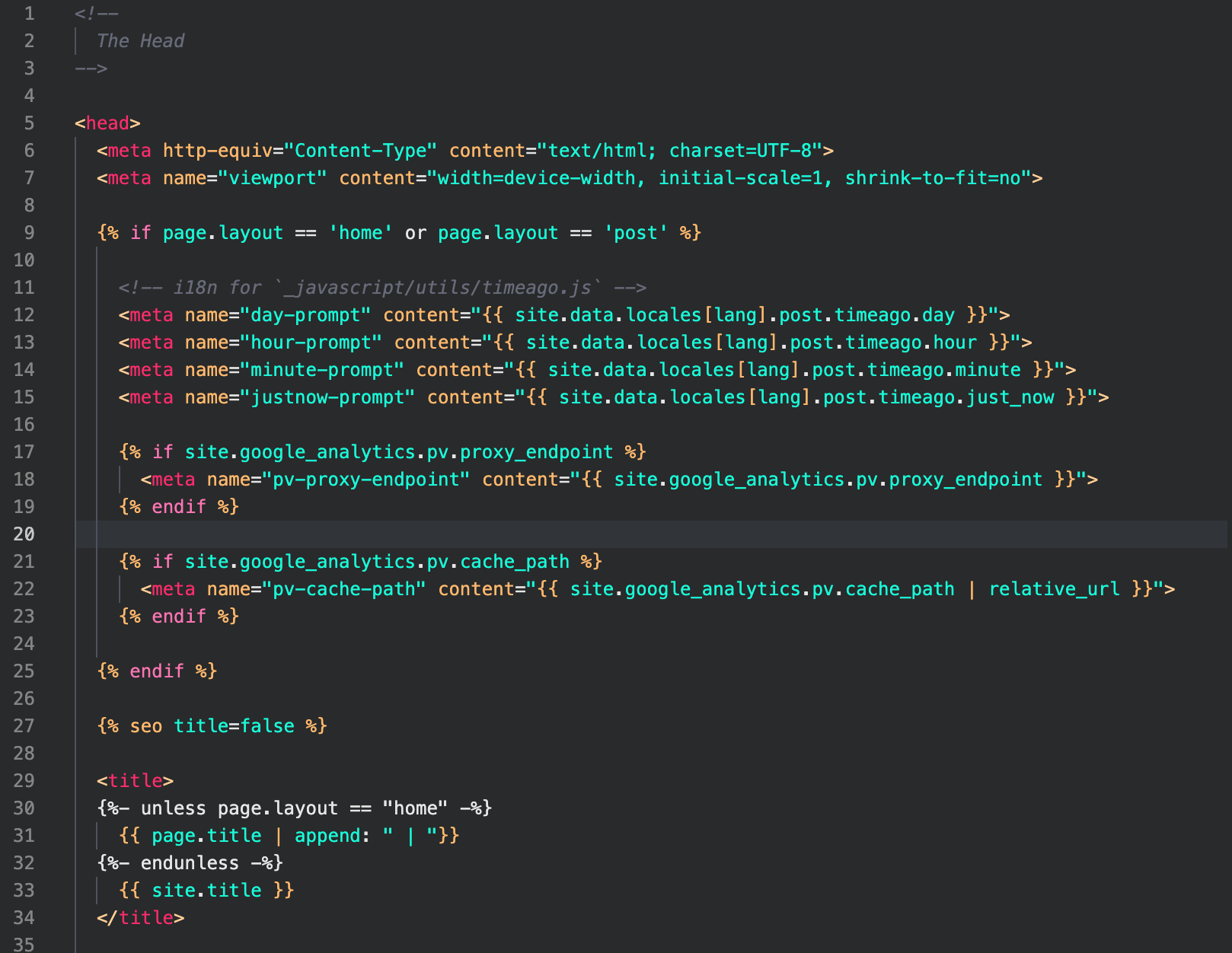blog head 태그 정보를 담고 있는 head.html의 일부

이 head.html에는 head태그에 들어가는 여러 javascript와 같은 세팅들이 포함되어 있습니다.
따라서 다른 파일을 모두 건드릴 필요없이 새로운 CDN 기반의 애드온들을 추가하고 싶으면 이 파일에 코드 한줄만 추가/수정하면 됩니다.
예시 코드의 9번 줄을 보면 코드에 {% %}를 사용한 코드가 있는데 이 코드는 지킬의 전반적인 구성을 하는 liquid 언어가 동작되는 영역입니다. 이 부분 코드는 대략적으로 해석하면 page는 현재 페이지를 의미하고 그에 대해 여러가지 세팅 변수를 가져오는 것으로 이해했습니다.
~~실제 자세히 분석은 안하고 대략적으로 필요할 때마다 체크합니다…~~
테마를 커스터마이징 할 때 팁이라면 우선 자신이 수정하고 싶은 부분을 크롬 개발자 모드(F12)등으로 페이지 분석을 합니다. 보통 디자인적 요소를 고치고 싶은 경우가 많아서 CSS파일 건드리는 경우가 많습니다. 예를 들어 어제 인용구 부분을 수정했었는데, 수정하고 싶은 부분을 Ctrl(cmd)+Shift+클릭 하면 해당 부분의 웹페이지 구성 코드를 볼 수 있습니다.

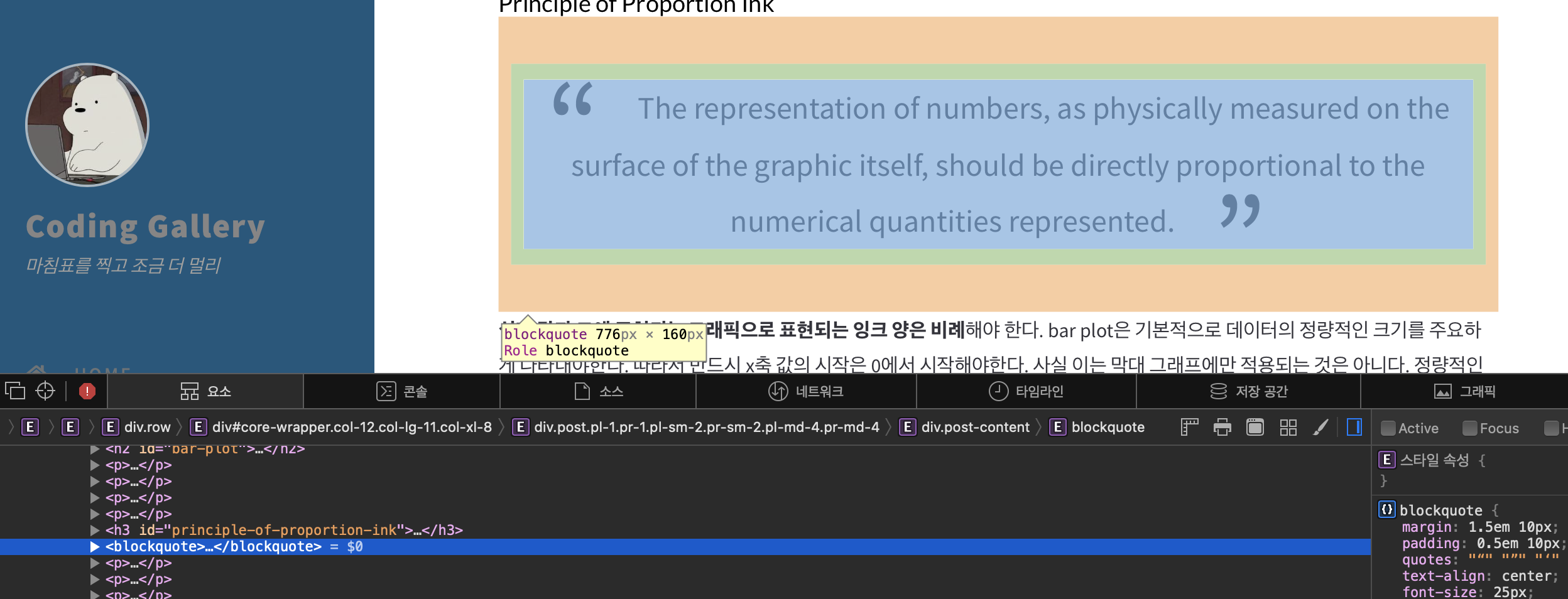
이렇게 찾은 부분의 태그를 폴더에서 검색으로 찾으면 연관된 코드를 찾을 수 있습니다.
그 후 해당 코드와 관련된 파일들을 수정하면서 변경사항을 체크하면됩니다.
변경사항 체크시 항상 깃에 푸시해서 체크하기가 어렵기 때문에 local mode로 페이지를 로드하고 supervisor모드로 해서 라이브로 수정된 변경사항을 볼 수 있는 방식으로 수정을 많이 합니다.

bundle exec jekyll serve s

MathJax

MathJax는 MathML, LaTex를 활용해 마크 업 종류의 언어로 웹 페이지에 수학식을 표기해주는 자바스크립트 라이브러리입니다.
자바스크립트 라이브러리기 때문에 head부분에 cdn으로 구성된 JS 링크를 추가해줘야하는데, MathJax 설치 세팅은 검색해보시면 더 잘 나와있으므로 Skip…
사실 블로그마다 js 라이브러리 코드를 입력하는 파일이 달라서 잘 찾아서 넣으시면됩니다.

MathJax Setting

기본적으로 MathJax 세팅을 알려드리겠습니다.
저같은 경우 파일 검색으로 MathJax를 해서 라이브러리 세팅코드가 된 부분을 찾았는데 없다면 javascript가 적용되는 파일을 찾아서 아래처럼 세팅해주시면 됩니다.

  
{% if page.math %}
  <!-- MathJax -->
  <script>
  /* see: <https://docs.mathjax.org/en/latest/options/input/tex.html#tex-options> */
  MathJax = {
    loader: {load: ['[tex]/color']},
    tex: {
      inlineMath: [              /* start/end delimiter pairs for in-line math */
        ['$','$'],
        ['\\(','\\)']
      ],
      displayMath: [             /* start/end delimiter pairs for display math */
        ['$$', '$$'],
        ['\\[', '\\]']
      ],
      packages: {'[+]':['color']}
    }
  };
  </script>
  <script src="https://polyfill.io/v3/polyfill.min.js?features=es6"></script>
  <script type="text/javascript" id="MathJax-script" async
    src="https://cdn.jsdelivr.net/npm/mathjax@3/es5/tex-chtml.js">
  </script>
{% endif %}

코드에서 가장 중요한 부분은 tex: 부분입니다. 이 부분에서 inlineMath와 displayMath의 명령어 세팅을 진행하는데, 보통 기본 세팅은 \\(과 \\[을 사용하는 방식이지만 편리성을 위해 많이들 $를 사용하는 방식을 씁니다.
inlineMath란 지금 글에 적힌 것처럼 $1 + 2 = 3$ 과 같이 글 내부에 수식을 넣는 방식을 말합니다.
displayMath란 글과 글 사이 간격에 공간을 차지하여 넓게 작성하는 방식입니다.

\[1 + 2 = 3\]

그리고 밑에 있는 packages는 제가 컬러를 표현하기위해 직접 추가한 코드인데, 이런 추가적인 세팅은 MathJax공식 도규먼트에 사용법이 나와있습니다.

자주 쓰는 수식

제가 자주 쓰는 수식들을 작성하는 방식을 설명하겠습니다.

Basic

\[\begin{aligned} ||\mathbf{x} - \mathbf{y}||_2 = ||\mathbf{y} - \mathbf{x}||_2 \\\\ \cos\theta = \frac{< \mathbf{x}, \mathbf{y} >}{||\mathbf{x}||_{2}||\mathbf{y}||_{2}} \end{aligned}\]

  
$$
\begin{aligned}
    ||\mathbf{x} - \mathbf{y}||_2 = ||\mathbf{y} - \mathbf{x}||_2 \\\\
    \cos\theta = \frac{< \mathbf{x}, \mathbf{y} >}{||\mathbf{x}||_{2}||\mathbf{y}||_{2}}
\end{aligned}
$$

기본적으로 알아두면 좋은 것들입니다.
가장 기본적으로 _{}와 ^{}는 각각 밑첨자, 윗첨자입니다. 중괄호로 묶지 않으면 바로 다음에 나타나는 문자만 인식하므로 대체로 중괄호를 쓰는 걸 추천합니다.
일반적으로 삼각함수 용어들은 \text{cos} 등의 형태로 글을 정자로 작성하게 해주는 \text{}를 쓰기도 하는데 보통 \cos, \sin, \log 등 여러분이 생각하는 대부분의 표현은 이미 존재합니다.
분수를 표현하는 방식 중 가장 직관적인 표현 방법을 쓰려면 \frac{}{}을 쓰면됩니다. 왼쪽 중괄호는 분자, 오른쪽 중괄호는 분모입니다.
\mathbf{}는 글자를 표현하는 방식입니다. 벡터는 일반적으로 위에 화살표는 긋는 경우($\vec{X}$ a.k.a \vec{})도 많지만 굵은 글씨로 표현하는 경우($\mathbf{X}$)가 더 많습니다. 이때 사용하는 것이 \mathbf{}입니다.

Vector

ML/DL 뿐 아니라 통계학 공부와 포스팅을 할 때 벡터를 사용하는 경우가 많습니다.
부캠 Vector에서도 벡터 수식을 굉장히 잘 쓴 것을 볼 수 있는데 작성 요령을 설명드리겠습니다.

\[\begin{aligned} \mathbf{X} = \begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix} \quad \mathbf{X} = \begin{bmatrix} 1 & 2 & 3 \end{bmatrix} \end{aligned}\]

  
$$
\begin{aligned}
    \mathbf{X} = \begin{bmatrix}
    1 \\
    2 \\
    3
    \end{bmatrix}
    \quad
    \mathbf{X} = \begin{bmatrix}
    1 & 2 & 3
    \end{bmatrix}
\end{aligned}
$$

기본적으로 줄바꿈은 \\을 사용하는데, 이를 적용하기 위해서는 반드시 \begin{aligned} 설정을 해야합니다.
벡터에서 줄바꿈은 \\를 쓰면되고 같은 칸을 맞춰 정렬할 때는 &를 쓰면 됩니다.
띄어쓰기의 경우 \; 등 여러가지가 있는데 이게 칸이 매우 미세하게 조정되기 때문에 저는 보통 \quad나 \qquad를 씁니다.
행렬 혹은 벡터 표현에 사용되는 괄호는 디자인에 따라 명령어가 다릅니다. 사용하는 종류는 pmatrix, bmatrix, Bmatrix, vmatrix, Vmatrix 정도가 많이 사용됩니다.
그리고 이건 모든 displayMath에서 통용되는 것인데, \begin과 \end의 묶음이 하나의 줄을 차지합니다. 따라서 세로로 이어서 적고 싶으시다면 \begin{aligned}안에 새롭게 \begin{aligned}로 묶고 처리하셔도 됩니다.

\[\begin{aligned} \mathbf{X} = \begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \end{bmatrix} \quad\quad \begin{aligned} L_{1} : ||\mathbf{X}||_{1} = \sum_{i=1}^{d}|x_{i}| \\ L_{2} : ||\mathbf{X}||_{2} = \sqrt{\sum_{i=1}^{d}|x_{i}|^{2}} \end{aligned} \end{aligned}\]

  
$$
\begin{aligned}
    \mathbf{X} = \begin{bmatrix}
    x_{1} \\
    x_{2} \\
    x_{3} 
    \end{bmatrix}
    \quad\quad
    \begin{aligned}
    L_{1} : ||\mathbf{X}||_{1} = \sum_{i=1}^{d}|x_{i}| \\
    L_{2} : ||\mathbf{X}||_{2} = \sqrt{\sum_{i=1}^{d}|x_{i}|^{2}}
    \end{aligned}
\end{aligned}
$$  

시그마를 쓰고 싶으실땐, \sigma를 적으시면 $\sigma$가 나옵니다. 이때는 \sum을 적으면 됩니다.
참고로 말씀드리면 inlineMath모드에서는 bar(|)를 쓰고 싶으시다면 반드시 앞에 역슬래쉬 (\)를 붙여주셔야 인식이 됩니다.

Matrix

\[\begin{aligned} \mathbf{X} = \begin{bmatrix} \mathbf{x}_1 \\ \mathbf{x}_2 \\ \mathbf{x}_3 \\ \vdots \\ \mathbf{x}_n \end{bmatrix} = \begin{bmatrix} x_{11} & x_{12} & ... & x_{1m} \\ x_{21} & x_{22} & ... & x_{2m} \\ \vdots & \vdots & x_{ij} & \vdots \\ x_{n1} & x_{n2} & ... & x_{nm} \end{bmatrix} = (x_{ij}) \end{aligned}\]

  
$$
\begin{aligned}
\mathbf{X} = \begin{bmatrix}
        \mathbf{x}_1 \\
        \mathbf{x}_2 \\
        \mathbf{x}_3 \\
        \vdots \\
        \mathbf{x}_n
    \end{bmatrix}
    =
    \begin{bmatrix}
    x_{11} & x_{12} & ... & x_{1m} \\
    x_{21} & x_{22} & ... & x_{2m} \\
    \vdots & \vdots & x_{ij} & \vdots \\
    x_{n1} & x_{n2} & ... & x_{nm}
    \end{bmatrix}
    = (x_{ij})
\end{aligned}
$$

행렬은 벡터의 연장선이라 크게 달라진 것은 없습니다. 같은 간격을 맞춰 열을 조정하려면 &, 행을 조정하려면 \\을 씁니다.
조금 참고할만한 내용은 가로, 세로, 대각선 점표시입니다. 이때는 \vdots, \cdots, \ddots를 적으면 됩니다. 각각 vertical, column, diagonal의 약자인 것 같습니다.

Long Expressions

대체로 저는 길게 수식을 적는걸 선호하진 않습니다. 이게 간지?는 나는데 적는 사람입장에선 굉장히 헷갈립니다. 우선 간단한 긴 식을 보여드리겠습니다.

\[\begin{matrix} \theta^{(t+1)} & \leftarrow & \theta^{(t)} - \hat{\nabla_{\theta} \mathcal{L}}(\theta^{(t)}) \\\\ & \Downarrow& \\\\ \beta^{(t+1)} & \leftarrow & \beta^{(t)} + \frac{2 \lambda}{b}\mathbf{X}^\intercal_{(b)}\left( \mathbf{y}_{(b)} - \mathbf{X}_{(b)}\beta^{(t)} \right) \end{matrix}\]

  
$$
\begin{matrix}
    \theta^{(t+1)} & \leftarrow & \theta^{(t)} - \hat{\nabla_{\theta} \mathcal{L}}(\theta^{(t)}) \\\\
    & \Downarrow& \\\\
    \beta^{(t+1)} & \leftarrow & \beta^{(t)} + \frac{2 \lambda}{b}\mathbf{X}^\intercal_{(b)}\left( \mathbf{y}_{(b)} - \mathbf{X}_{(b)}\beta^{(t)} \right)
\end{matrix}
$$

뭔가 여러가지가 많이 들어갑니다. 일단 이런 수식들은 정렬을 가지런히 맞추는 것이 중요합니다. 따라서 \begin{matrix}를 활용해 괄호가 없는 행렬의 방식으로 작성합니다.
행렬 작성에서 &가 열을 정렬해준다고 했는데, 이 원리를 사용합니다.
즉 쉽게 말하면 수식 묶음 하나하나가 하나의 행렬의 열에 들어간다고 생각하면됩니다.
제가 앞서 긴 수식은 한 흐름에 잘 안적는다고 했는데 이게 이유가 있습니다…

\[\begin{aligned} \begin{aligned} \text{(1)}\quad\quad\quad\quad\;\;\; \partial_{\beta_{k}}||\mathbf{y} - \mathbf{X}\beta||_{2} = \partial_{\beta_{k}}\left\{ \frac{1}{n}\sum^{n}_{i=1}\left( y_{i} - \sum_{j=1}^{d}X_{ij}\beta_{j} \right)^2 \right\}^{1/2} \end{aligned} \\\\ \begin{matrix} \text{(2)}\quad\quad\quad \nabla_{\beta} ||\mathbf{y} - \mathbf{X}\beta||_{2} &=& (\partial_{\beta_{1}}||\mathbf{y} - \mathbf{X}\beta||_{2}, ..., \partial_{\beta_{d}}||\mathbf{y} - \mathbf{X}\beta||_{2} ) \\ &=& \left( -\frac{\mathbf{X}^{\intercal}_{\cdot 1}(\mathbf{y}-\mathbf{X}\beta)}{n||\mathbf{y}-\mathbf{X}\beta||_{2}}, ..., -\frac{\mathbf{X}^{\intercal}_{\cdot d}(\mathbf{y}-\mathbf{X}\beta)}{n||\mathbf{y}-\mathbf{X}\beta||_{2}} \right) \\ &=& -\frac{\mathbf{X}^{\intercal}(\mathbf{y}-\mathbf{X}\beta)}{n||\mathbf{y}-\mathbf{X}\beta||_{2}} \\\\ &\Downarrow& \\\\ \beta^{(t+1)} & \leftarrow & \beta^{(t)} - \lambda\nabla_{\beta}||\mathbf{y} - \mathbf{X}\beta^{(t)}|| \\ &=& \beta^{(t)} + \frac{\lambda}{n}\frac{\mathbf{X}^{\intercal}(\mathbf{y}-\mathbf{X}\beta^{(t)})}{||\mathbf{y}-\mathbf{X}\beta^{(t)}||_{2}} \\ \end{matrix} \\ \end{aligned}\]

이런 수식 적으려면 코드가 어마어마해집니다… 코드 첨부하면 너무 길어져서… 캡쳐로 대체하겠습니다.

[BoostCamp AI Tech / 심화포스팅] Jekyll Blog와 MathJax