[BoostCamp AI Tech / Level 1 - AI Math] Day4 - RNN 첫 걸음

AI Math : RNN 첫걸음

---

Sequence 데이터

1. 개념

• 소리, 문자열, 주가와 같이 일련의 흐름이 존재하는 데이터
  • 시계열(time series) 데이터는 시간 순서에 따라 나열하므로 sequence data에 속한다.
• sequence data는 독립동등분포(i.i.d) 가정을 위배하는 경우가 많으므로 순서가 변경되거나 과거 정보의 손실이 발생하면 데이터의 확률분포가 변경된다.

2. sequence data handling

\[\begin{aligned} \begin{matrix} P(X_1, ..., X_t) &=& P(X_t | X_1, ... X_{t-1})P(X_1, ..., X_{t-1}) \\ &=& P(X_t | X_1, ... X_{t-1})P(X_{t-1}|X_1, ..., X_{t-2})P(X_1, ..., X_{t-2}) \\ &=& \prod_{s=1}^{t}P(X_s | X_{s-1}, ..., X_1) \end{matrix} \end{aligned}\]

• 기본적인 원리가 이전 시퀀스의 정보를 가지고 앞으로 발생할 데이터의 확률분포를 다루기 위해 조건부확률을 이용할 수 있다는 것이다.

\[\begin{aligned} X_{t} \sim P(X_t | X_{t-1}, ..., X_1) \quad\quad \\ X_{t+1} \sim P(X_{t+1} | X_{t}, X_{t-1}, ..., X_1) \end{aligned}\]

• 시퀀스 데이터는 데이터의 길이가 가변적이기 때문에 모델 자체도 가변길이에 대응할 수 있는 모델로 설계되어야한다.
• 조건부에 들어가는 데이터의 길이를 조절하는 방식의 모델을 자기회귀(AR)모델이라고 말한다.

\[\begin{aligned} X_{t} \sim P(X_t | {\color{orange}{X_{t-1}, ...}}, X_1) \quad\quad \\ X_{t+1} \sim P(X_{t+1} | {\color{orange}{X_{t}, X_{t-1}}}, ..., X_1) \end{aligned} \quad \text{Let } {\color{orange}{orange}} \text{ is } \tau\]

• 고정된 길이 $\tau$ 만큼의 시퀀스만 사용하는 경우를 $AR(\tau)$ (Autoregressive Model) 자기회귀모델이라 한다.

\[\begin{aligned} X_{t} \sim P(X_t | X_{t-1}, H_t) \quad \\ X_{t+1} \sim P(X_{t+1} | X_{t}, H_{t+1}) \end{aligned} \quad\quad H_t = \text{Net}_{\theta}(H+{t-1}, X_{t-1})\]

• 바로 이전의 정보를 제외한 나머지 정보들을 $H_t$라는 잠재변수로 인코딩해서 활용하는 잠재 AR모델이다.

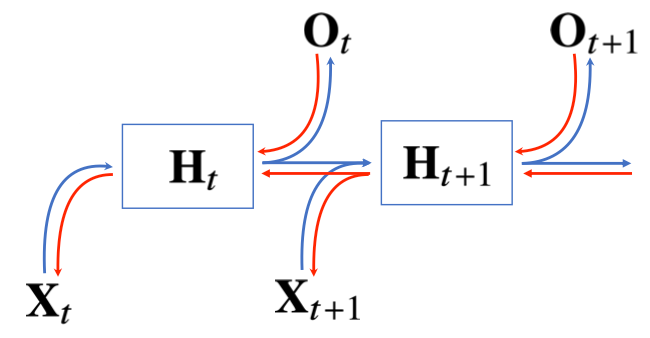
Recurrent Neural Network (RNN)

1. RNN 기본원리

\[\begin{aligned} \mathbf{H}_t = \begin{cases} \sigma(\mathbf{X}_t\mathbf{W}^{(1)} + \mathbf{b}^{(1)}) &&&& \text{MLP} \\ \sigma(\mathbf{X}_t\mathbf{W}^{(1)}_{X} + \mathbf{H}_{t-1}\mathbf{W}^{(1)}_{H} + \mathbf{b}^{(1)}) &&&& \text{RNN} \end{cases} \\\\ \mathbf{O} = \mathbf{HW}^{(2)} + \mathbf{b}^{(2)} \quad\quad\quad\quad\quad\quad\quad \\ \end{aligned}\]

• 변수
  • $\mathbf{H}$ : 잠재변수
  • $\sigma$ : 활성화함수
  • $\mathbf{W}$ : 가중치행렬
  • $\mathbf{b}$ : bias
• RNN의 기본적인 형태는 MLP와 유사한 모형이다.
• 단, 기본적인 MLP는 이전 값을 활용할 수 없기에 이전 잠재변수를 활용한다.
  • 즉, 이전 순서의 잠재변수가 현재의 입력으로 들어온다는 것이다.

2. RNN의 역전파

• RNN의 역전파는 단순 역전파와는 다른 형태로 진행된다.
• 근본적으로 편미분을 통해 backpropagation을 하는 것은 같지만 단순 역전파를 하기엔 무리가 있다.
• RNN의 역전파는 Backpropagation Through Time (BPTT)라고 한다.

3. 수식을 통한 BPTT

\[\begin{aligned} L(x, y, w_h, w_o) = \sum_{t = 1}^{T}l(y_t, o_t) \quad\quad\quad h_t = f(x_t, h_{t-1}, w_h) \text{ and } o_t = g(h_t, w_o) \end{aligned}\]

• BPTT는 각 가중치행렬에 들어가는 미분값을 모두 계산하고 한번에 update를 진행한다.
• 우선 각 시점에 대해 prediction과 label의 차를 계산하는 $l(y_t,o_y)$를 위와 같이 정의한다.

\[\partial_{w_{h}}L(x, y, w_h, w_o) = \sum_{t=1}^{T}\partial_{w_h}l(y_t, o_t) = \sum_{t=1}^T\partial_{o_t}l(y_t, o_t)\partial_{h_t}g(h_t , w_h)[\partial_{w_h}h_t]\]

• $W_h$에 대해 손실함수를 편미분을 진행한다. 이때 왜 $O_t$와 $h_t$에 대해 편미분이 진행되냐면 $w_h$로는 바로 $o_t$를 편미분할 수 없다. 즉 아래와 같은 과정이 발생한다.

\[\frac{\partial L}{\partial w_h} = \frac{\partial L}{\partial o_t}\frac{\partial o_t}{\partial h_t}\frac{\partial h_t}{\partial w_h}\]

• 기본적인 gradient descent 원리인 chain rule에 의해 동작하기 때문에 추가적인 편미분 표현이 나타난 것이다.
• 이후 단순히 여기서만 끝나는 것이 아닌 $h_t$도 $w_h$를 포함한 함수이므로 속미분에 의해 $W_h$에 의해 편미분을 진행해야한다.

\[\partial_{w_h}h_t = \partial_{w_h}f(x_t, h_{t-1}, w_h) + \sum_{i=1}^{t-1}\left( \prod_{j=i+1}^{t} \partial_{h_{j-1}}f(x_j, h_{j-1}, w_h)\partial_{w_h}f(x_i, h{i-1}, w_h) \right)\]

• 이 과정에서도 $h_t$에 있는 또다른 $h_{t-1}$에 의해 다시 연속적인 속미분이 진행된다. 이런 결과로 계속해서 값이 곱해지는데 이 경우 대부분 가중치는 소수점을 갖는 경우가 많기 때문에 곱연산이 많을수록 0에 수렴하게된다.
• 이를 기울기 소실 (vanishing gradient)라고 한다.

기울기 소실의 해결책

• 기울기 소실이 발생하는 이유는 너무 과도한 재귀형태의 연산이 발생하기 때문이다.
• 기울기 소실의 해결책으로는 시퀀스의 길이를 끊어버리는 truncated BPTT를 사용한다.

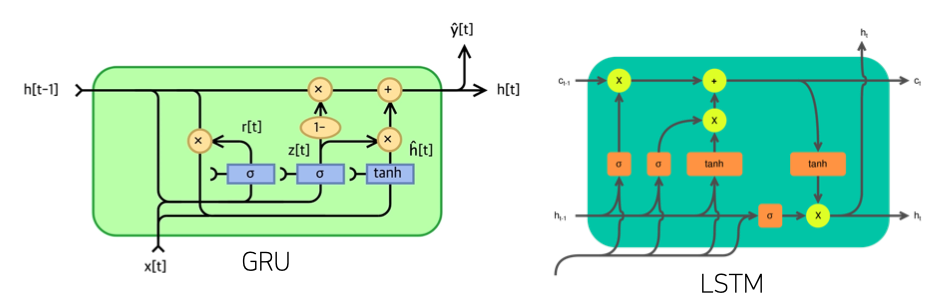
• 또한 이를 근본적으로 해결하고자 LST, GRU와 같은 네트워크들이 등장했다.