[BoostCamp AI Tech / Level 1 - AI Math] Day4 - CNN 첫 걸음

AI Math : CNN 첫걸음

---

Convolution 연산 이해하기

1. MLP

\[h_{i} = \sigma\left( \sum_{j=1}^{p} W_{ij}x_{j} \right)\]

• 기존의 다층 신경망(MLP)은 fully connected 구조이기 때문에 각 성분 $h_{i}$에 대응하는 가중치 행 $\mathbf{W}_{i}$가 필요
  • 이런 이유로 성분의 수가 많아지면 가중치행렬의 크기와 parameter의 크기가 너무 크다는 문제가 발생

2. Convolution

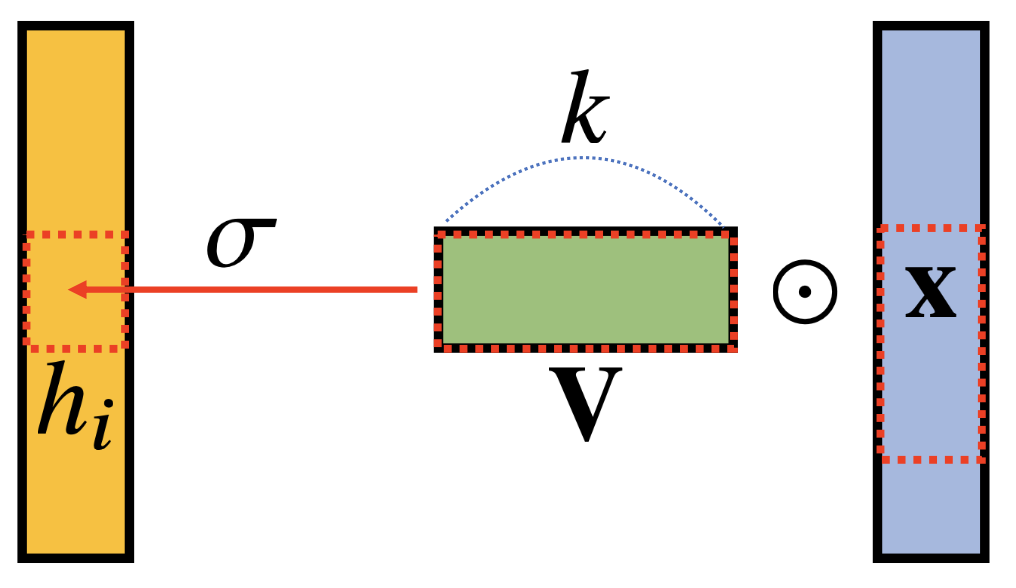
\[h_{i} = \sigma\left( \sum_{j=1}^{k}V_{j}x_{i+j-1} \right)\]

• convolution 연산의 기본원리는 기존의 가중치행렬을 사용하는 것이 아닌 kernel을 활용하는 구조
  • kernel은 고정된 가중치 행렬
• convolution 연산의 수학적 의미는 신호를 커널을 통해 국소적 증폭 또는 감소하여 정보를 필터링 하는 것

\[\begin{aligned} \text{continuous} \quad [f * g](x) = \int_{\mathbb{R}}f(z)g(x \pm z)dz = \int_{\mathbb{R}}f(x \pm z)g(z)dz = [g * f](x) \\ \text{discrete} \quad [f * g](x) = \sum_{a\in\mathbb{Z}^{d}}f(a)g(i \pm a) = \sum_{a\in\mathbb{Z}^{d}}f(i \pm a)g(a) = [g * f](i) \quad\quad \end{aligned}\]

• CNN에서 사용되는 연산은 convolution이라 하지 않고 cross-correlation이라 한다.
• 단순히 1차원에서만 가능한 연산이 아니고 다차원에서도 가능한 연산이다.
• 데이터 종류에 따른 convolution 연산
  • 음성/text : 1-D
  • 영상 : 2-D, 3-D

2차원 Convoluton 이해하기

\[\text{2-D Conv} \quad\quad [f * g](i, j) = \sum_{p, q}f(p, q)g(i+p, j+q)\]

• 단순히 수식만으로는 convolution 연산을 이해하기는 어렵다. 간단한 예제를 통해 2차원 convolution을 이해해보자.

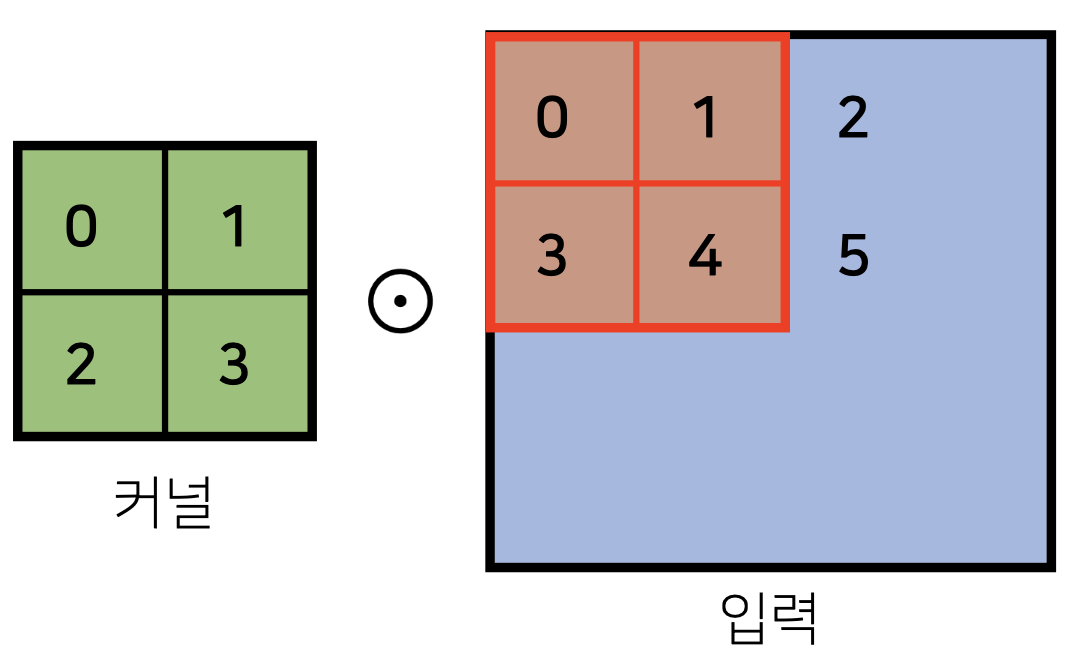
• 커널은 항상 동일하게 주어진다. 이후 입력값에 대해 커널을 겹쳐서 각 행렬값을 element-wise 방식으로 연산한다.
• 간단히 말하면 입력벡터 위를 커널이 지정된 step-wise에 맞춰 이동하는 것이다,
• 이렇게 연산한 방식으로 나온 결과는 다음과 같다.
  
• 여기서 step-wise가 1이라면 다음은 [1, 2, 4, 5 ] 와 커널의 element-wise 값을 계산한다.
• convolution 연산에서 가장 중요한 것은 입력의 크기와 커널의 크기를 통해 출력의 크기를 계산하는 것이다. 이를 알아야 데이터의 축소, 확장을 자유자재로 연산할 수 있기 때문이다.

\[\begin{aligned} O_{H} = H - K_{H} + 1 \; \\ O_{W} = W - K_{W} + 1 \end{aligned}\]

• 예를 들어 입력이 28X28이고 커널이 3X3이라면 2D-Conv 연산을 진행하면 26X26이 된다.
• 채널이 여러개인 2차원 입력인 경우 2차원 convolution을 채널 개수만큼 적용한다.

\[\sum_{i=1}^{n}{K_{i} \text{Input}_{i}} \quad\quad K_{i} : \text{i-th Kernel}\]

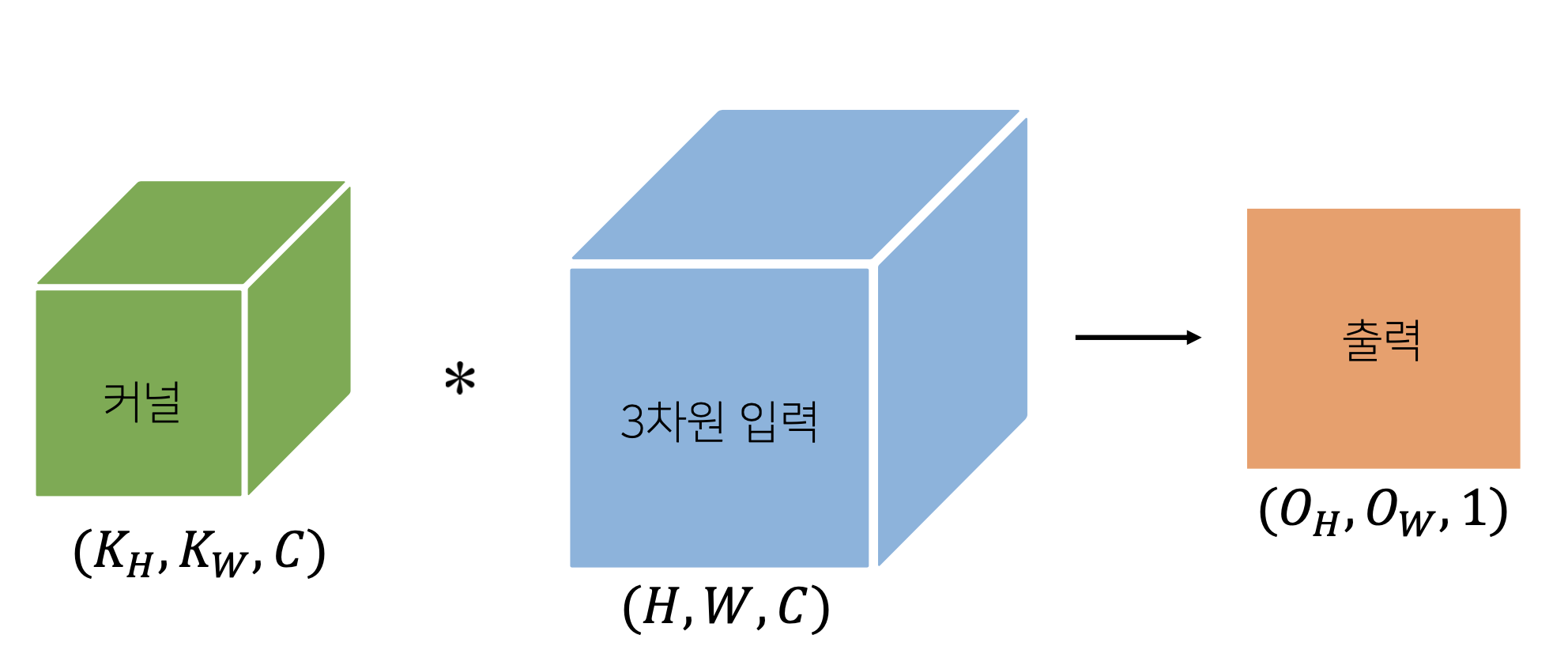
• 위의 연산은 좀 더 단순하게 보면 직육면체 블록같은 텐서의 커널와 텐서의 입력으로 convolution 연산을 하는 것과 같다.

Convolution 역전파

\[\begin{aligned} \begin{matrix} \frac{\partial}{\partial x}[f * g](x) &=& \frac{\partial}{\partial x}\int_{\mathbb{R}^{d}}f(y)g(x-y) dy \\ &=& \int_{\mathbb{R}^{d}}f(y)\frac{\partial g}{\partial x}(x - y)dy \\ &=& [f * g'](x) \end{matrix} \end{aligned}\]

• Convolution 연산은 커널이 모든 입력 데이터에 공통으로 적용되기 때문에 역전파를 계산할 때도 convolution 연산이 나오게 된다.
• 역시나 수식 자체보다는 그림으로 이해하는게 편하다.

\[o_i = \sum_{j}w_{j}x_{i+j-1}\]

• CNN의 기본 convolution 연산은 커널의 이동에 기반한 element-wise 값들의 연산이다.
  결국 backpropagation을 위해서는 각 출력에 들어온 특정 입력($x_i$)과 특정 가중치 ($W_i$)를 활용해야한다.

• backpropagation의 기본원리는 출력에 들어온 값을 활용해서 미분을 통해 가중치를 갱신하는 것이다.
• 각 convolution 출력에 맞는 loss의 미분값을 계산했다고 하자.

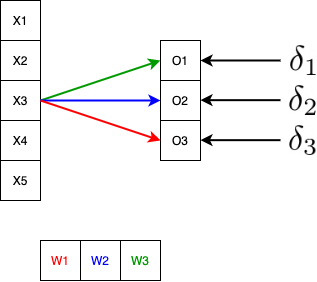
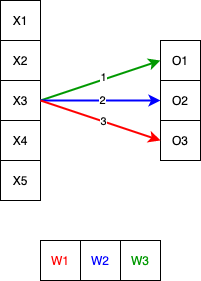
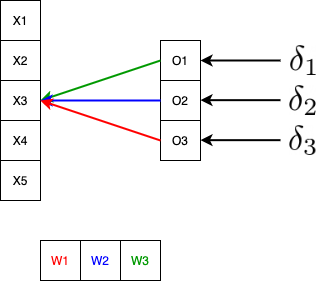
• $x_3$은 커널 $W_1$, $W_2$, $W_3$을 한번씩 거치게 된다. 물론 $x_3$과 특정 커널의 곱 결과는 서로 다른 출력을 보이기 때문에 각 출력에 맞는 미분값 $\sigma$를 각 커널에 곱한 것은 $x_3$이 기여한 결과이다.
• $\delta_1 \color{green}{w_{3}}$ + $\delta_2 \color{blue}{w_{2}}$ + $\delta_3 \color{red}{w_{1}}$

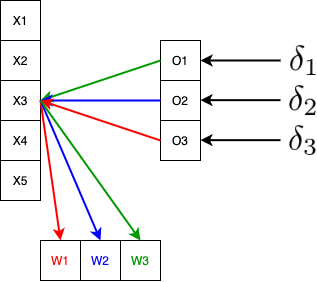
• 이렇게 계산된 미분값을 가중치 업데이트에 활용하는데, 각 가중치에는 각 출력에 알맞은 미분값 $\delta$와 해당 값을 연산하는데 기여한 $x_i$의 곱연산을 활용하여 업데이트한다.
• 사실 결과적으로보면 역으로 convolution 연산을 하는 것과 같다.
• 커널의 gradient update : $(\color{red}{\delta_3 x_e}, \color{blue}{\delta_2 x_3}, \color{green}{\delta_1 x_3})$

\[\frac{\partial L}{\partial w_i} = \sum_{j}\delta_{j}x_{i+j-1}\]

• 최종적으로 커널의 각 가중치에 사용되는 loss function의 편미분 연산값은 각 커널 가중치를 사용한 모든 convolution 연산에 사용된 입력과, 해당 출력의 미분값의 곱들의 합이 된다. 적고 나서 다시 읽어봤는데 겁나 헷갈린다.