AI Math : 확률론 맛보기
Introduction
- 딥러닝은 확률론 기반의 기계학습 이론
- 회귀분석 : $L_{2}$-norm은 예측오차의 분산을 최소화하는 방향
- 분류문제 : Cross Entropy는 모델의 불확실성을 최소화하는 방향
용어정의
1. 데이터 공간
- 데이터 $(\mathbf{x}, y) \sim D$
- $D$는 이론적 확률분포
2. 확률변수
- 이산확률변수 (discrete random variable)
- 확률변수가 가질 수 있는 모든 경우의 수를 합한 것
- 연속확률변수 (continuous random variable)
- 확률변수의 밀도 위에서 적분
- 정확한 확률을 구하는 것은 불가능하기 때문
확률분포
1. 결합분포 (joint distribution)
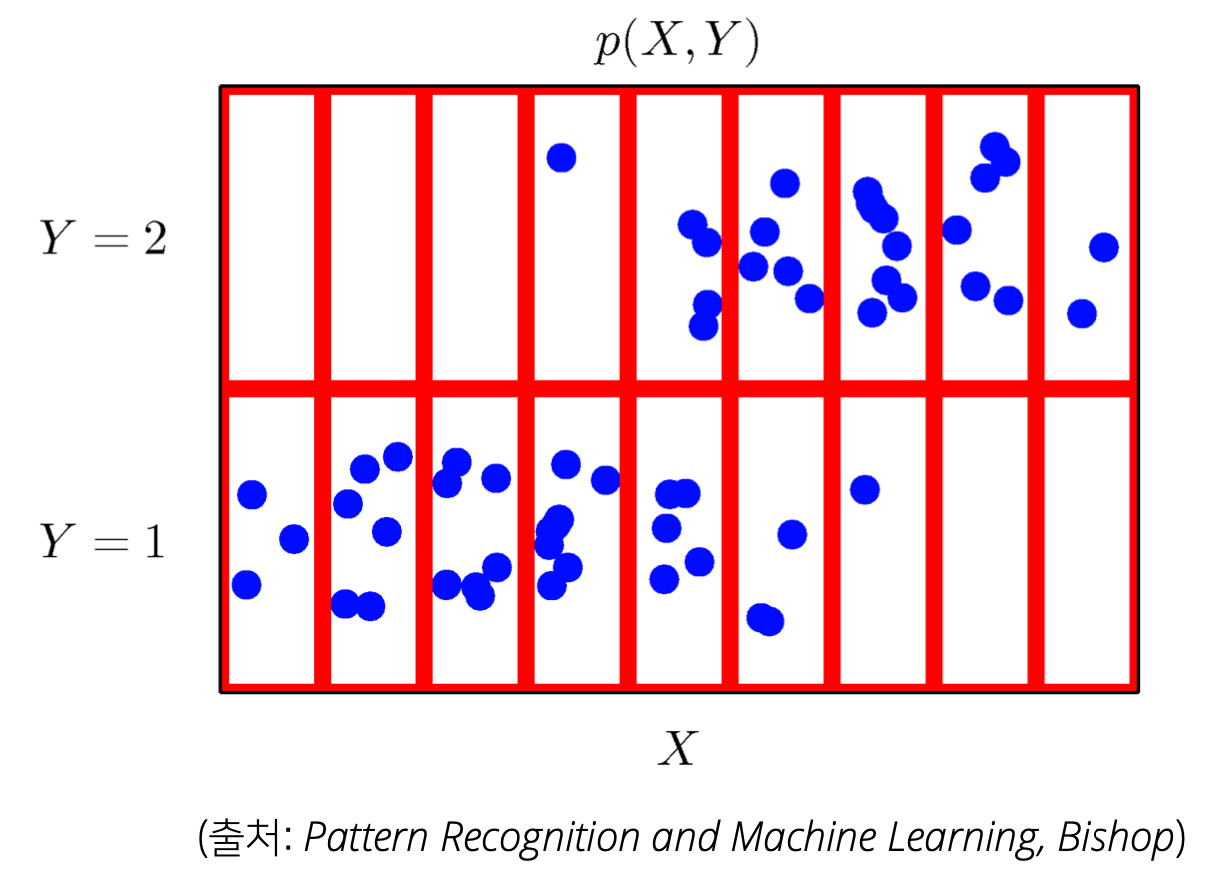
- 각 $X$와 $Y$에 따라 구분하여 동시에 고려한 분포를 형성
$\Rightarrow$ $P(\mathbf{x}, y)$는 $D$를 모델링함 - 확률변수가 여러 개일때 함께 고려하는 확률분포
2. 주변확률분포 (marginal distribution)
\[P(\mathbf{x}) = \sum_{y}P(\mathbf{x}, y) \text{ or } \int_{y}P(\mathbf{x}, y) dy\]- $\mathbf{x}$에 대한 정보를 표현한 것
- 위에 있는 사진의 데이터를 기준으로 설명을 하면 나눠진 9개의 칸을 왼쪽부터 1 ~ 9라고 하면 X가 1일때 점의 개수, 2일때 점의 개수 같은 것을 주변확률분포라고 한다.
3. 조건부확률분포
\[P(\mathbf{x} | y)\]- 입력 $\mathbf{x}$와 출력 y의 관계를 모델링한다.
- 특정 클래스 $y$가 주어졌을 때, $\mathbf{x}$의 확률분포를 의미
기대값이란?
\[\begin{aligned} \mathbb{E}_{\mathbf{x} \sim P(\mathbf{x})}[f(\mathbf{x})] = \int_{\chi} f(\mathbf{x})P(\mathbf{x})d\mathbf{x} \quad\quad\quad\quad\text{(continuous)}\\ \mathbb{E}_{\mathbf{x} \sim P(\mathbf{x})}[f(\mathbf{x})] = \sum_{\mathbf{x} \in \chi} f(\mathbf{x})P(\mathbf{x})d\mathbf{x} \quad\quad\quad\quad\quad\text{(discrete)} \end{aligned}\]- $f$에 다른 수식을 넣으면 다양한 통계량을 구할 수 있음
- 분산 : $\mathbb{V}(\mathbf{x}) = \mathbb{E}_{\mathbf{x} \sim P(\mathbf{x})}[(\mathbf{x} - \mathbb{E}[\mathbf{x}])^2]$
- 첨도 : $\text{Skewness}(\mathbf{x}) = \mathbb{E}\left[ \left( \frac{\mathbf{x} - \mathbb{E}[\mathbf{x}]}{\sqrt(\mathbb{V}(\mathbf{x}))} \right)^3 \right]$
- 분산
\(\text{Cov}(\mathbf{x}_1, \mathbf{x}_2) = \mathbb{E}_{\mathbf{x}_1,\mathbf{x}_2 \sim P(\mathbf{x}_1\mathbf{x}_2)}[(\mathbf{x}_1 - \mathbb{E}[\mathbf{x}_1])(\mathbf{x}_2 - \mathbb{E}[\mathbf{x}_2])]\)
조건부확률과 기계학습
$ P(y | \mathbf{x}) $ : 입력 $\mathbf{x}$ 가 들어왔을 때 정답이 $\mathbf{y}$ 일 확률
로지스틱 회귀에서는 선형모델 + softmax를 사용
- 추출된 패턴을 기반으로 확률을 해석함
분류문제
$softmax(\mathbf{w}\phi + \mathbf{b})$은 데이터 $\mathbf{x}$ 로부터 추출된 특징패턴 $\phi({\mathbf{x}})$과 가중치행렬 $\mathbf{W}$ 을 통해 조건부확률 $P(y |\mathbf{x})$을 계산- 회귀문제
조건부기대값 $\mathbb{E}[y|\mathbf{x}]$ 을 추정함
$\mathbb{E}_{y \sim P(y|\mathbf{x})}[y|\mathbf{x}] = \int_y yP(y|\mathbf{x})dy$ - 왜 조건부기대값을 계산하는가?
- 공식연산 결과가 $L_{2}$-norm의 최소화 식과 일치함
몬테카를로 샘플링
\[\mathbb{E}_{\mathbf{x} \sim P(\mathbf{x})}[f(\mathbf{x})] \approx \frac{1}{N}\sum_{i=1}^{N}f(\mathbf{x}^{(i)}) \quad,\quad \mathbf{x}^{(i)} \stackrel{iid}{\sim} P(\mathbf{x})\]- 확률분포를 모를때 기대값 계산을 위해 Monte Carlo Sampling이 필요함
example
\[\begin{aligned} \begin{matrix} \int_{-1}^{1} e^{-x^2} dx = \text{?} \\ \frac{1}{2}\int_{-1}^{1}e^{-x^{2}}dx \approx \frac{1}{N}\sum_{i=1}^{N}f(x^{(i)}) \quad,\quad x^{(i)} \sim U(-1, 1) \end{matrix} \end{aligned}\]- 이 과정에서 적분구간 길이가 2이므로 균등분포의 추출을 위해 2로 나눔

Comments powered by Disqus.