RecSys : Bandit for Recommendation

Multi-Armed Bandit (MAB)

One-Armed Bandit

카지노의 슬롯머신을 돌리는 상황
one-armed를 외팔이 강도라고 하는데, 좀 더 이해를 돕고자하면 확률이 일정한 슬롯머신을 돌리는 상황임
- 예를 들면 동전 던지기
만약 이런 슬롯머신이 K개 존재한다면 어떻게 할까?

Multi-Armed Bandit

제한된 횟수 N번동안 K개의 슬롯머신을 돌려서 최대의 이익을 찾는 문제
단, k개의 슬롯머신은 모두 다른 보상과 모두 다른 확률 분포를 갖고 있음
- 쉽게 말하면 probablistic distribution을 갖는 게임이 k개 있는 것
- ex) 동전 던지기, 주사위 굴리기 가 함께 있는 상황
이때 고려할 것은 크게 2가지
- 어떤 상황에서 어떤 머신을 작동할 지 (policy)
- 머신들을 어떤 순서로 동작할 지

MAB의 문제와 논점

MAB의 문제는 슬롯머신의 reward 확률을 정확하게 알 수 없다는 것임
- 확률 분포를 갖는 경우 굉장히 큰 시도를 진행하면 수렴을 할 수 있지만 제한된 횟수만 진행하므로 이를 알기는 어려움
- 따라서 수행 정책을 세우고 이에 따라 진행해야 함
- 정책은 방향성으로 구분하면 크게 2가지로 구분
MAB 정책
- Exploration (탐색)
  - 더 많은 정보를 얻고자 새로운 arm을 동작
  - 모든 슬롯머신을 비슷하게 당기는 것
  - 탐색에 비용이 많이 들기 때문에 높은 reward를 얻기는 어려움
- Exploitation (활용)
  - 슬롯 머신을 몇 번 댕겨보면서 남은 횟수동안은 제일 높은 확률인 것 같은(경험, 관측) 슬롯머신에 몰빵
  - 좋은 정책으로 생각될 수 있으나 잘못된 exploitation이면 오히려 reward가 감소
  - 예를 들어 내가 가장 높다고 생각한 슬롯머신 바로 옆이 더 높은 reward일 수도 있는 것
이런 trade-off 문제가 발생하기 때문에 exploration과 exploitation의 적절한 균형점을 찾아야 함

MAB 공식

\[q_{*}(a) \doteq \mathbb{E}[R_t \mid A_t = a]\]

Notations
- $t$ : time step, play number
- $A_t$ : $t$에 수행한 action
- $R_t$ : $t$에 받은 reward
- $q_*(a)$ : action a에 따른 reward의 실제 기대값
정확한 $q_*(a)$를 아는 게 가장 좋지만 treu distribution을 알기는 어려움
이에 따라 추정치인 $Q_t(a)$를 최대한 비슷하게 구하는 것이 목표
- 추정을 최대로 하는 action을 선택하는 것을 greedy action이라 함
- greedy action : exploitation
- 새로운 action : exploration

MAB Algorithm

MBA 알고리즘은 어떻게 action을 수행할 지 policy를 결정함

Greedy Algorithm

\[\begin{aligned} Q_{t}(a) \doteq \frac{\text{sum of rewards when } a \text{taken prior to } t}{\text{number of times} a \text{taken prior to } t} = \frac{\sum_{i=1}^{t-1} R_i \cdot \mathbf{1}_{A_i=a}}{\sum_{i=1}^{t-1} \mathbf{1}_{A_i=a}} \\\\ A_t = \underset{a}{\text{argmax}} Q_t(a) \qquad\qquad\qquad\qquad\qquad \end{aligned}\]

가장 기본적인 연산방식으로 각 머신들의 표본 평균을 활용
가장 간단한 policy로 평균 reward가 최대가 되는 것을 선택
문제점
- policy가 처음 선택되는 action과 reward에 큰 영향을 받음
  - 특정 action의 초반 reward가 낮으면 배제될 수도 있음
  - 이런 문제는 exploration이 부족한 단점이 발생할 수 있음

Epsilon-Greedy Algorithm

\[A_t = \begin{cases} \underset{a}{\text{argmax}} Q_t (a) \quad \text{with probability } 1 - \epsilon \\ \text{a random action} \quad \text{with probability } \epsilon \end{cases}\]

greedy algorithm의 단점인 exploration을 해결하는 policy
일정 확률로 슬롯머신을 랜덤으로 선택함
문제점
- 시행 횟수가 커지면 true distribution에 근접하는데, 항상 $\epsilon$ 확률의 랜덤 샘플이 나오므로 후반부에는 손해가 날 수도 있음

Upper Confidence Bound (UCB)

\[A_t \doteq \underset{a}{\text{argmax}} \left[ Q_t(a) + c\sqrt{\frac{\ln t}{N_t(a)}} \right]\]

notations
- $t$ : time step, play number
- $Q_t(a)$ : t시간에 수행한 action a에 대한 reward 추청 (simple average)
- $N_t(a)$ : action a를 선택한 횟수
- $c$ : exploration을 조정하는 하이퍼파라미터
새로 추가된 term은 action의 선택 확률을 조정해줌
- action a의 선택 수 $\downarrow$ $\Rightarrow$ 분몬 $\downarrow$ $\Rightarrow$ 불확실성 $\uparrow$ $\Rightarrow$ a에 대한 확률 $\uparrow$ $\Rightarrow$ action 선택 확률 $\uparrow$

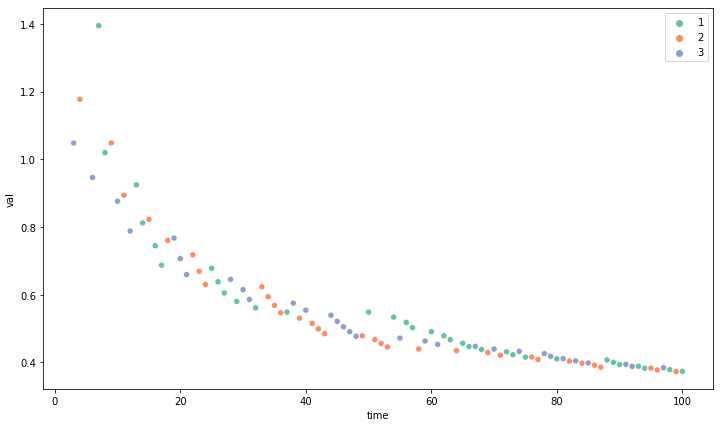슬롯이 3개인 상황에서 랜덤으로 슬롯머신을 추출하여 추가된 항의 변화 그래프

실제로는 확률이 적용되어 랜덤하게 슬롯이 선택되진 않지만 action의 선택수가 증가하면 실제로 매우 낮은 값으로 수렴하는 것을 볼 수 있음
결국 특정 action a가 많이 선택되면 추가된 항이 0에 수렴하기 때문에 기존의 simple average가 됨

결론

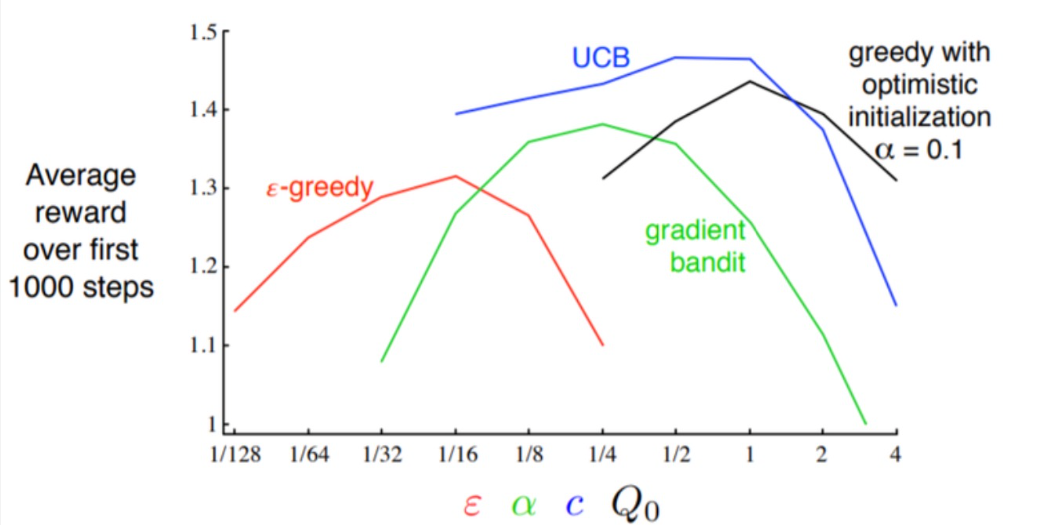“Reinforcement Learning: An Introduction – Second edition, in progress”, p48

실제로 UCB가 전반적으로 좋은 성능을 보이나 실제로는 적절한 exploration과 exploitation의 균형을 이루는 것이 중요

MAB를 추천에 적용한 경우

서비스 지표인 클릭/구매를 모델의 reward로 가정
reward를 최대화하는 방향으로 학습을 진행
무겁지 않은 간단한 bandit에도 CTR, CVT 지표가 좋아짐
개별 아이템을 action으로 구분
유저에게 아이템을 추천하는 방식을 MAB에서 policy
- exploration : 변화하는 유저의 취향 탐색, 아이템 후보 확장
- exploitation : 유저 취향의 아이템을 추천
사용자의 클릭여부를 MAB의 reward로 사용함

문제점과 해결방안

유저 추천
- 개별 유저별로 처리를 할 경우 데이터 수의 부족으로 bandit(슬롯머신)의 수렴을 하기 어려운 문제가 있음
- 클러스터링으로 유저를 그룹화하여 그룹별 bandit을 구축함
  - bandit수 = 유저 클러스터 수 X 후보 아이템 수
아이템 추천
- 주어진 아이템과 유사한 후보 리스트로 bandit을 적용
- 유사 추출은 MF, item2vec 등으로 계산

MAB 알고리즘 - 심화

Thompson Sampling

k개의 action에 해당하는 확률분포를 구하는 문제
각 action 추정치는 $\beta$ 분포를 따른다는 가정을 함

\[Beta(x \mid \alpha, \beta) = \frac{1}{B(\alpha, \beta)}x^{\alpha-1}(1-x)^{\beta - 1}\]

초기상태는 $Beta(1, 1)$로 세팅
각 배너들을 랜덤하게 노출하면서 초기 세팅을 형성 (그냥 $Beta(1,1)$로 해도 괜찮은듯 함)
1. 이때, 클릭하면 $\alpha + 1$, 클릭하지 않으면 $\beta + 1$
어느정도 분포가 형성이 되면 각 배너의 값에 맞춰 베타분포에서 샘플을 추출
추출된 샘플에서 가장 높은 확률의 배너를 노출
1. 이때, 클릭하면 $\alpha + 1$, 클릭하지 않으면 $\beta + 1$
3~4를 많은 수로 노출

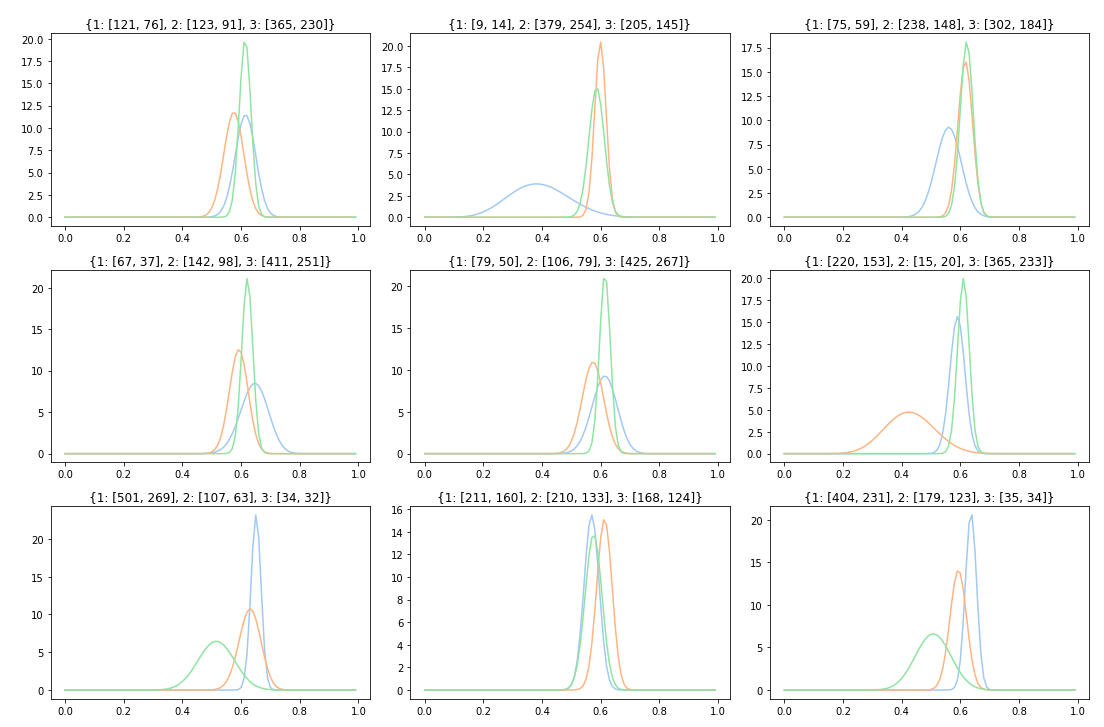
총 9번의 케이스를 1000회 노출을 진행한 후 각 아이템별 베타분포
좀 더 현실적으로 재현하고자 광고 미클릭 확률이 클리보다 높게 설정함

  
fig, axes = plt.subplots(3, 3, figsize=(15, 10))

for ax in axes.flatten():
    x = [i/100 for i in range(0, 100)]

    banners = {
        1 : [1, 1],
        2 : [1, 1],
        3 : [1, 1]
    }

    cases = {
        1 : [],
        2 : [],
        3 : []
    }

    for i in range(1000):
        samples = np.array([np.random.beta(a, b) for a, b in banners.values()])
        idx = np.argmax(samples) + 1
        view = np.random.randint(5) % 2
        banners[idx][view] += 1

    for k, v in banners.items():
        sns.lineplot(x=x, y=sp.beta(banners[k][0], banners[k][1]).pdf(x), ax=ax)
        ax.set_title(str(banners))

plt.tight_layout()
plt.show()

LinUCB

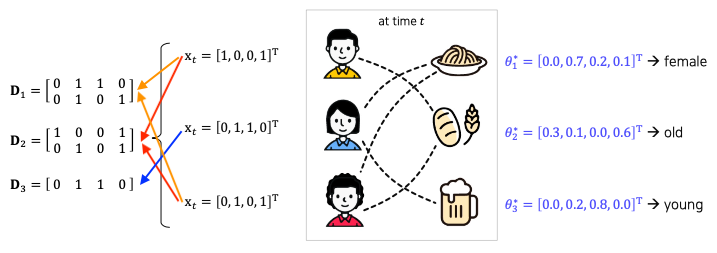
\[A_t \doteq \underset{a}{\text{argmax}}\left[ \mathbf{x}^\intercal_{t,a}\theta^*_a + \alpha\sqrt{\mathbf{x}^\intercal_{t,a} \mathbf{A}^{-1}_a \mathbf{x}_{t,a}} \right], \quad \text{where } \mathbf{A}_a = \mathbf{D}^\intercal_a\mathbf{D}_a + \mathbf{I}_d\]

$\mathbf{x}_{t,a}$ : d-차원의 컨텍스트 벡터
- user, context feature (성별, 연령 등등… + item의 정보)
$\theta^*_a$ : action a에 대한 d 차원 학습 파라미터
- action별로 파라미터를 update
$\mathbf{D}_a$ : t 시점의 m개의 컨텍스트 벡터로 구성된 $m\times d$행렬
- context vector는 유저의 관찰 데이터 행렬
- $\mathbf{D}_i$는 i번째 아이템을 선택한 user $x$의 특징 벡터
파라미터가 업데이트되면 각 파라미터는 해당 아이템을 많이 소비한 특징들의 정보를 갖게됨

[BoostCamp AI Tech / RecSys] Day40 - Bandit for Recommendation