[BoostCamp AI Tech / Level 1 - AI Math] Day3 - 경사하강법 (매운맛)

AI Math : 경사하강법 (매운맛)

---

Introduction

• 선형모델은 무어-펜로즈를 사용해서 계산이 가능하지만 Gradient Descent로 계산을 많이 함
  • 목적식 : $|| \mathbf{y} - \mathbf{X}\beta||_{2}$
    $\Rightarrow$ 목적식을 최소화하는 $\beta$를 찾는 것이 목적이므로 $\beta$로 편미분 진행한다.
  • 무어-펜로즈 공식은 링크 참조

경사하강법 (Gradient Descent)

1. 공식

\[\begin{aligned} \begin{aligned} \text{(1)}\quad\quad\quad\quad\;\;\; \partial_{\beta_{k}}||\mathbf{y} - \mathbf{X}\beta||_{2} = \partial_{\beta_{k}}\left\{ \frac{1}{n}\sum^{n}_{i=1}\left( y_{i} - \sum_{j=1}^{d}X_{ij}\beta_{j} \right)^2 \right\}^{1/2} \end{aligned} \\\\ \begin{matrix} \text{(2)}\quad\quad\quad \nabla_{\beta} ||\mathbf{y} - \mathbf{X}\beta||_{2} &=& (\partial_{\beta_{1}}||\mathbf{y} - \mathbf{X}\beta||_{2}, ..., \partial_{\beta_{d}}||\mathbf{y} - \mathbf{X}\beta||_{2} ) \\ &=& \left( -\frac{\mathbf{X}^{\intercal}_{\cdot 1}(\mathbf{y}-\mathbf{X}\beta)}{n||\mathbf{y}-\mathbf{X}\beta||_{2}}, ..., -\frac{\mathbf{X}^{\intercal}_{\cdot d}(\mathbf{y}-\mathbf{X}\beta)}{n||\mathbf{y}-\mathbf{X}\beta||_{2}} \right) \\ &=& -\frac{\mathbf{X}^{\intercal}(\mathbf{y}-\mathbf{X}\beta)}{n||\mathbf{y}-\mathbf{X}\beta||_{2}} \\\\ &\Downarrow& \\\\ \beta^{(t+1)} & \leftarrow & \beta^{(t)} - \lambda\nabla_{\beta}||\mathbf{y} - \mathbf{X}\beta^{(t)}|| \\ &=& \beta^{(t)} + \frac{\lambda}{n}\frac{\mathbf{X}^{\intercal}(\mathbf{y}-\mathbf{X}\beta^{(t)})}{||\mathbf{y}-\mathbf{X}\beta^{(t)}||_{2}} \\ \end{matrix} \\ \end{aligned}\]

• 목적식을 $\begin{Vmatrix}\mathbf{y} - \mathbf{X}\beta^{(t)}\end{Vmatrix}^{2}_{2}$ 를 쓴다면 gradient는 다음과 같다.

\[\nabla_{\beta}\begin{Vmatrix}\mathbf{y} - \mathbf{X}\beta\end{Vmatrix}_{2}^{2} = -\frac{2}{n}\mathbf{X}^\intercal (\mathbf{y} - \mathbf{X}\beta)\]

• $\beta$로 편미분을 진행하는 의미를 좀 자세히 알아보자.
  미분을 하는 이유는 좌표계에서 함수값의 변화 방향성을 알기 위해서이다.
  위의 식에서 $\mathbf{X}$는 다변수로 존재하는 벡터 형식의 데이터인데, $\beta$는 $\beta_{1}$, $\beta_{2}$, …, $\beta_{d}$가 모여있는 벡터라고 보면 된다. 각 $\beta$가 담당하는 좌표계에서의 변수가 극솟값을 향하는 방향으로 연산을 하기위해 각 $\beta$에 맞추어 편미분을 진행하는 것이다.
  좀 더 수식적으로 바라보면 아래와 같다.
  \(\begin{aligned} \mathbf{X} = \begin{bmatrix} x_{11} & x_{12} & ... & x_{1n} \\ x_{21} & x_{22} & ... & x_{2n} \\ \vdots & \vdots & & \vdots \\ x_{m1} & x_{m2} & ... & x_{mn} \end{bmatrix} \quad \beta = \begin{bmatrix} \beta_{1} \\ \beta_{2} \\ \vdots \\ \beta_{n} \end{bmatrix} \quad \mathbf{X}\beta = \begin{bmatrix} x_{11}\beta_{1} & x_{12}\beta_{2} & ... & x_{1n}\beta_{n} \\ x_{21}\beta_{1} & x_{22}\beta_{2} & ... & x_{2n}\beta_{n} \\ \vdots & \vdots & & \vdots \\ x_{m1}\beta_{1} & x_{m2}\beta_{2} & ... & x_{mn}\beta_{n} \end{bmatrix} \end{aligned}\)
  여기서 $x_{ij}$는 $i$번째 데이터의 $j$번째 축값을 나타낸다고 생각하면 된다. 즉 한 줄의 행벡터는 n개 축을 갖는 좌표계에 있는 1개의 점을 의미한다.
  물론 여기서는 모든 $\beta$값이 동일하다고 보는게 맞는 것으로 본다.

• 어떻게 위의 gradient 계산값이 나온 건지는 너무 길기 때문에 접은 글에 적어두겠다.

gradient 공식 유도

위에서 편미분 값으로 활용된 $L_{2}$-norm을 풀어서 적으면 다음과 같다. $$ \begin{aligned} \begin{Vmatrix} \mathbf{y} - \mathbf{X}\beta \end{Vmatrix}_{2} = \sqrt{(y_{1} - x_{1}\beta_{1})^{2}+(y_{2} - x_{2}\beta_{2})^{2}+...+(y_{d} - x_{d}\beta_{d})^{2}} \end{aligned} $$ 위의 $L_{2}$-norm을 $\beta_{k}$에 대해 편미분을 하면 다음과 같이 계산된다. 고등학교때 배운 속미분을 활용하면된다. $$ \begin{aligned} \begin{matrix} \partial_{\beta_{k}} \begin{Vmatrix} \mathbf{y} - \mathbf{X}\beta \end{Vmatrix}_{2} &=& \partial_{\beta_{k}}\sqrt{(y_{1} - x_{1}\beta_{1})^{2}+(y_{2} - x_{2}\beta_{2})^{2}+...+(y_{d} - x_{d}\beta_{d})^{2}} \\ &=& \frac{1}{2}\left( \begin{Vmatrix} \mathbf{y} - \mathbf{X}\beta \end{Vmatrix}_{2} \right)^{-1} \times 2(-x_{k})(y_{k} - x_{k}\beta_{k}) \end{matrix} \end{aligned} $$ 이렇게 계산된 편미분은 결과적으로 다음과 같은 값을 갖게된다. ($x_{k}는 1차원인 경우 이고$ n차원인 경우는 $\mathbf{X}^{\intercal}_{\cdot k}$가 된다. 왜 전치행렬이 쓰이는지는 행렬을 작게 만들어서 차원비교 해보면 간단하게 확인 가능하다.) $$ \left( -\frac{\mathbf{X}^{\intercal}_{\cdot 1}(\mathbf{y}-\mathbf{X}\beta)}{n||\mathbf{y}-\mathbf{X}\beta||_{2}}, ..., -\frac{\mathbf{X}^{\intercal}_{\cdot d}(\mathbf{y}-\mathbf{X}\beta)}{n||\mathbf{y}-\mathbf{X}\beta||_{2}} \right) = -\frac{\mathbf{X}^{\intercal}(\mathbf{y}-\mathbf{X}\beta)}{n||\mathbf{y}-\mathbf{X}\beta||_{2}} $$

2. Gradient Descent Algorithm

Input : X, y, lr, T
Output : beta

Algorithm gradient_descent(lr, T)
    for t in range(T)
        error = y - X @ beta
        grad = -X.T @ error
        beta = beta - lr * grad

• eps 대신 T를 활용하여 학습횟수를 결정한다.
• learning rate (lr)과 학습횟수 (T)를 적절히 잘 조절하는 것이 중요하다.

확률적 경사하강법 (Stochastic Gradient Descent : SGD)

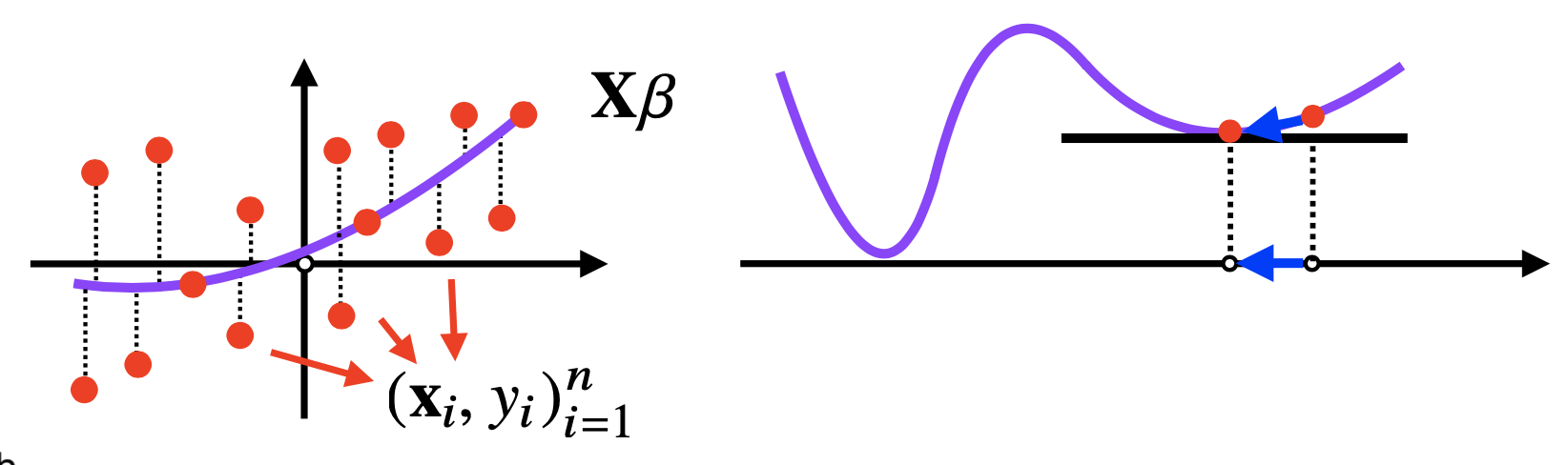
• 경사하강법은 선형회귀같은 미분가능하고 볼록(convex)하면 수렴이 보장된다.
  • $L_{2}$-norm 기반은 반드시 $\beta$에 대해 볼록이 보장된다.
• 비선형회귀는 목적식이 볼록하지 않을 수도 있다.
  $\Rightarrow$ 수렴이 보장되지 않음

1. SGD

\[\begin{matrix} \theta^{(t+1)} &\leftarrow& \theta^{(t)} - \hat{\nabla_{\theta} \mathcal{L}}(\theta^{(t)}) \\\\ &\Downarrow& \\\\ \beta^{(t+1)} &\leftarrow& \beta^{(t)} + \frac{2 \lambda}{b}\mathbf{X}^\intercal_{(b)}\left( \mathbf{y}_{(b)} - \mathbf{X}_{(b)}\beta^{(t)} \right) \end{matrix}\]

• 모든 data가 아닌 1개 또는 일부 data를 sampling하여 gradient를 계산하는 방식
  • 1개를 쓰면 SGD, 일부 data만 쓰면 mini-batch SGD라고 하지만 요즘 사용하는 SGD는 일반적으로 mini-batch SGD를 말한다.
• 이때, 모든 데이터 $(\mathbf{X}, \mathbf{y})$ 를 쓰지 않고 미니배치 데이터인 $(\mathbf{X_{(b)}, \mathbf{y}_{(b)}})$를 사용한다.
  • 이는 모든 데이터를 계산하는 것보다 연산량을 줄여준다.

2. Mini-batch

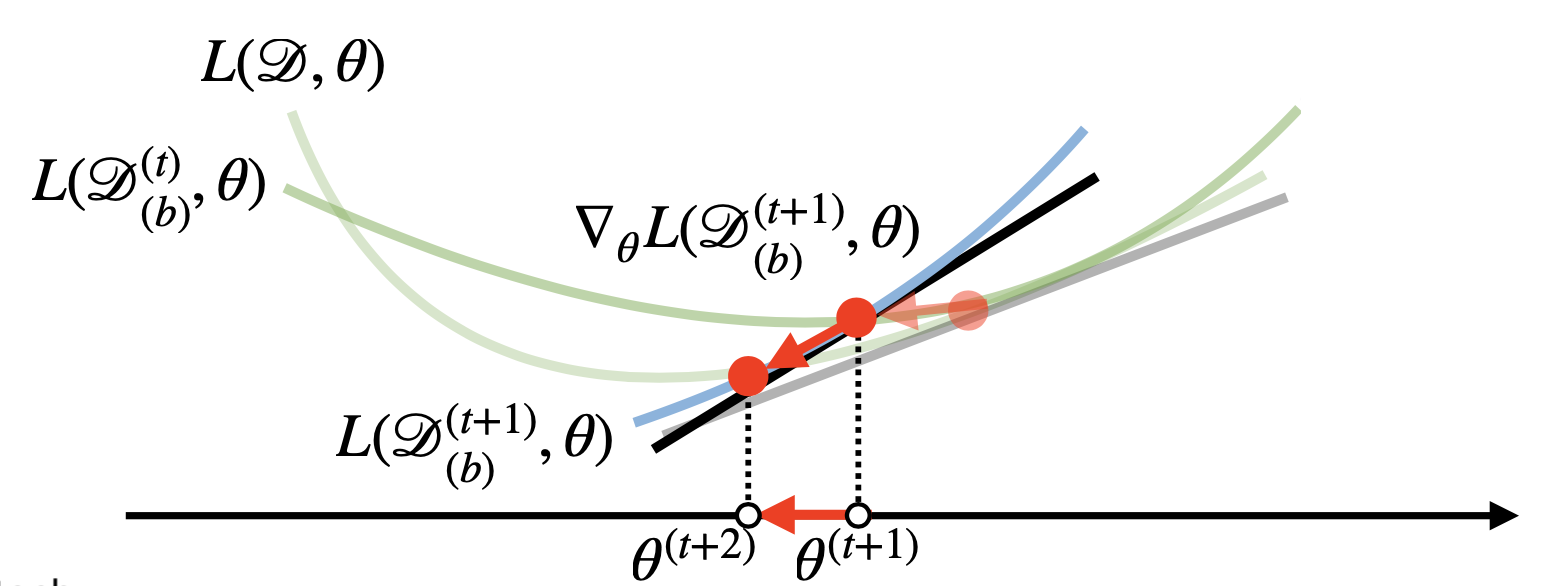
• SGD는 일부 데이터를 확률적(Stochastic)으로 sampling을 진행하므로 계산때마다 gradient를 계산하는 목적식이 바뀐다.
  $\Rightarrow$ local minimum을 탈출할 수 있다.
  $\Rightarrow$ 볼록함수가 아닌 목적식에도 사용가능하므로 더 효율적이다.
• learning rate, 학습횟수와 추가로 mini-batch size도 같이 고려할 필요가 있다.
• 병렬 연산이 가능하다
  • CPU : 데이터 전처리 작업 + GPU 작업용 데이터 준비
  • GPU : 행렬연산 + model parameter update