[BoostCamp AI Tech / Level 1 - AI Math] Day3 - 경사하강법 (순한맛)

AI Math : 경사하강법 (순한맛)

---

미분 (Differentiation)

\[f'(x) = \lim_{h \rightarrow 0}\frac{f(x+h) - f(x)}{h}\]

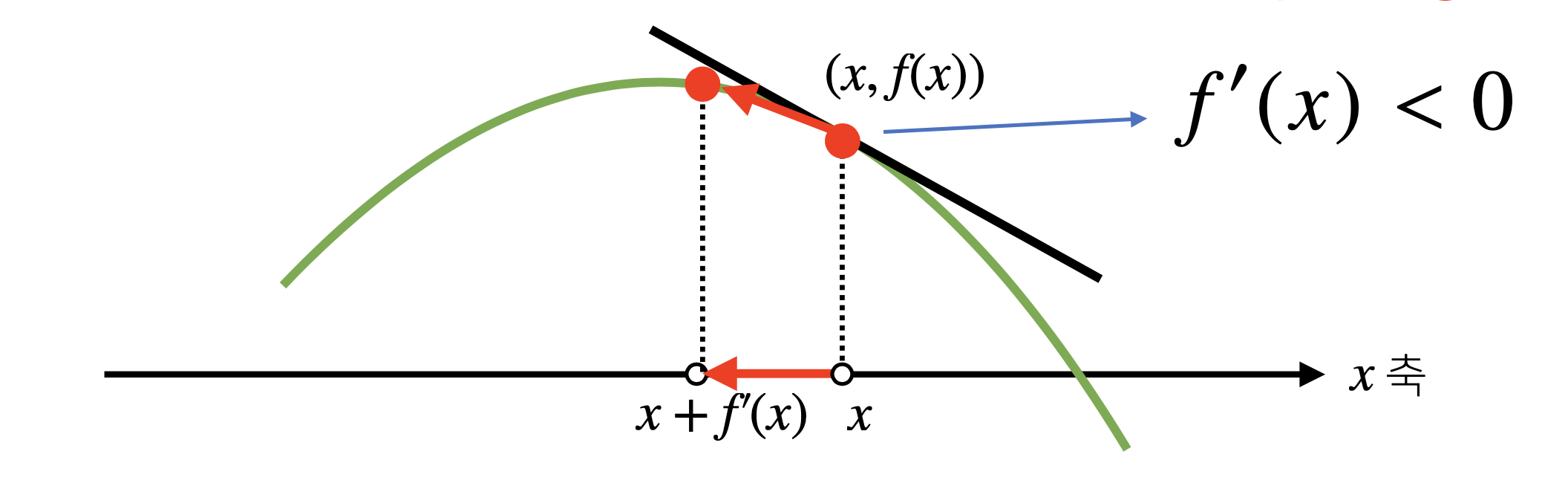
• 변수의 움직임에 따른 함숫값의 변화를 측정한다.
• ($x$, $f(x)$)에서의 접선의 기울기
• 최적화에 사용되는 연산
• sympy 모듈을 활용하면 미분값 계산이 가능하다
  • sympy.diff()

• 접선의 기울기 : 어떤 방향으로 가야 함수값을 증가/감소하는 지를 알려주는 역할

편미분 (Partial Differentiation)

\[\begin{aligned} \partial_{x_{i}}f(\mathbf{X}) = \lim_{h \rightarrow 0}\frac{f(\mathbf{X} + h\mathbf{e}_{i}) - f(\mathbf{X})}{h} \\\\ \nabla f = \left( \partial_{x_{1}}, \partial_{x_{2}}, ..., \partial_{x_{d}} \right) \quad\quad \end{aligned}\]

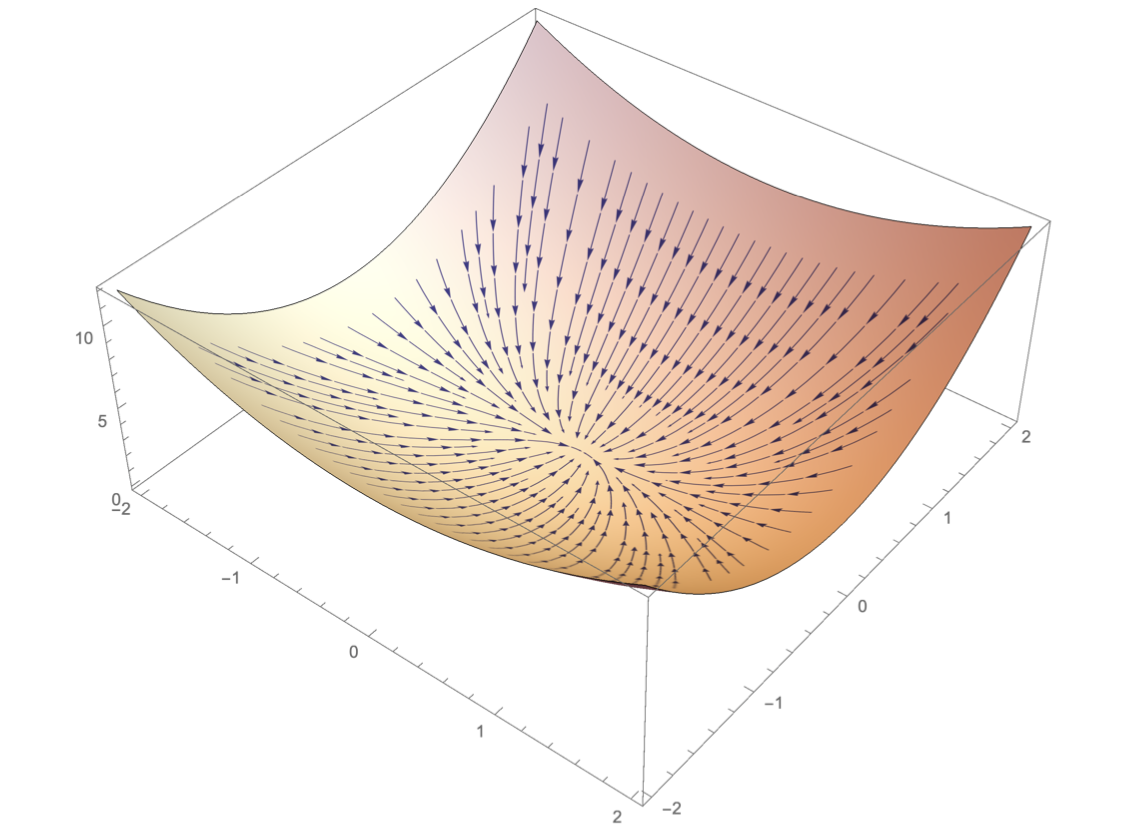
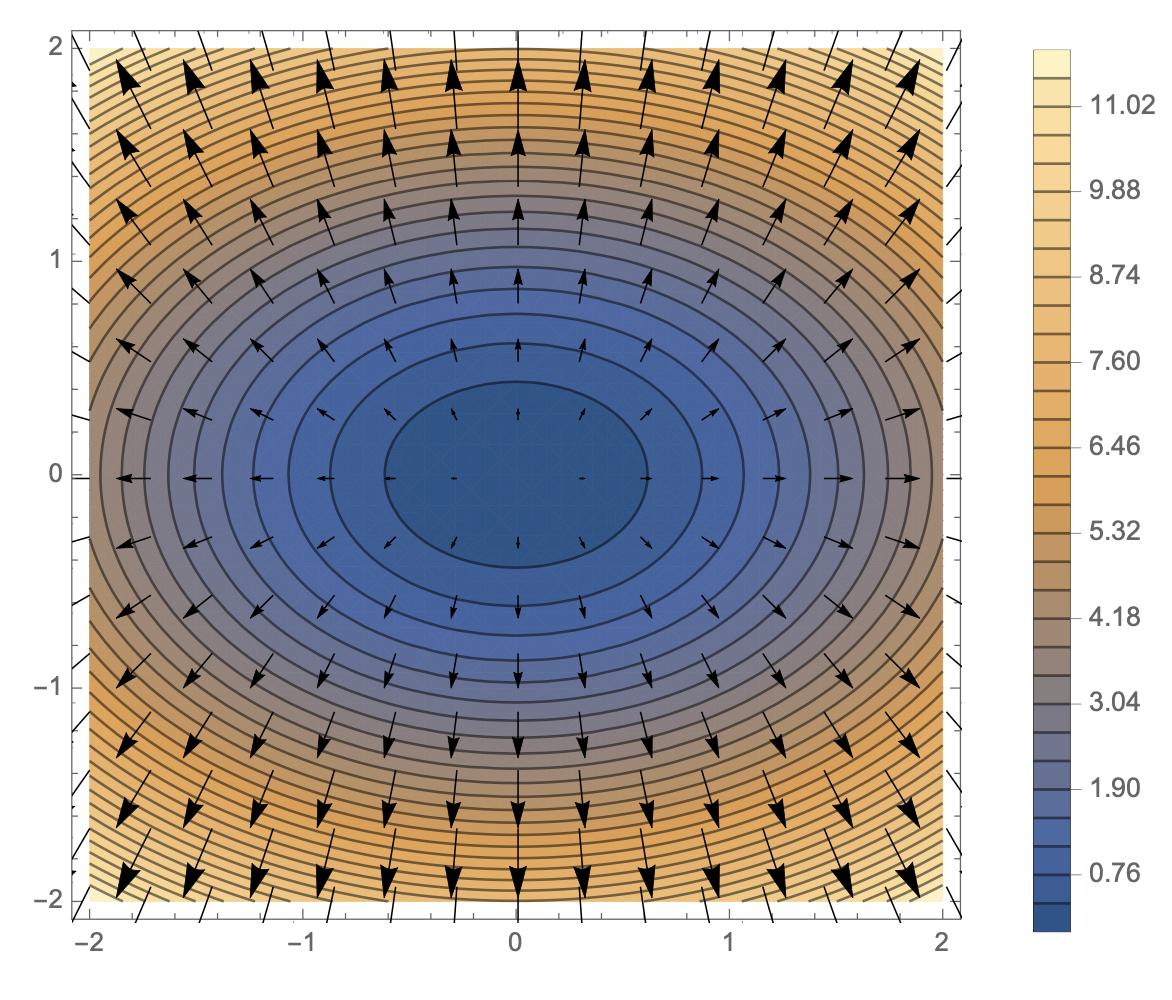
• 변수가 벡터와 같은 다변수인 경우 편미분을 활용
• $\nabla f$의 의미는 가장 빨리 증가하는 방향을 의미한다.
  따라서 $-\nabla f$는 가장 빠르게 감소하는 방향을 의미한다.
• 변수별로 편미분을 계산한 gradient 벡터를 사용한다.
• n차원에서는 특정 극점으로 향하는 것
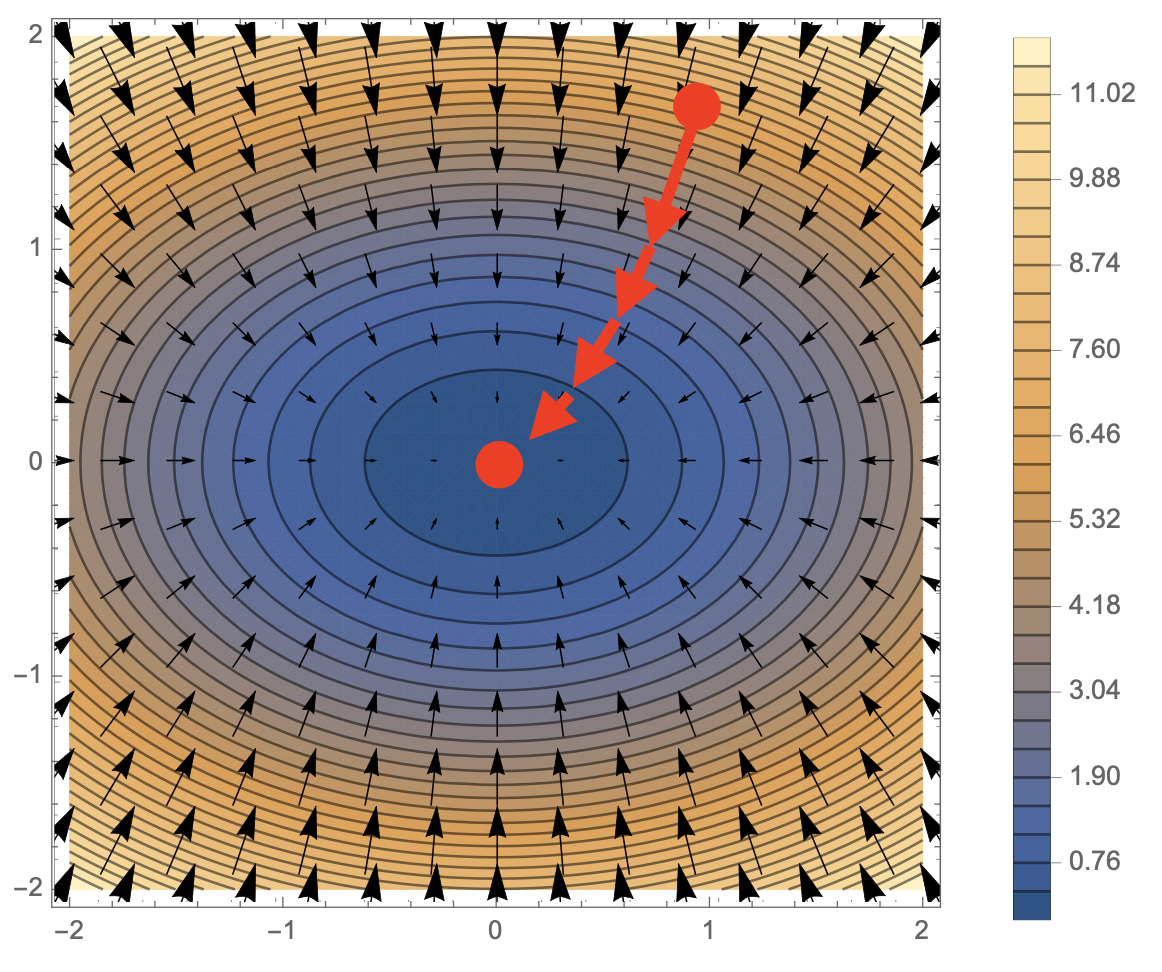
  • $-\nabla f$는 극소점으로 향한다.
    

경사하강법 (Gradient Descent)

• 미분값을 빼는 계산을 하는 것을 경사하강법(Gradient Descent)라고 한다.
  • 극솟값의 위치를 구함
  • 목적함수를 최소화
  • 극값에 도달한다면 $f’(x) = 0$이므로 gradient 연산 update를 중지한다.

Gradient Descent Algorithm

1. 단일변수

Input : gradient, init, lr, eps
Output : var

Algorithm gradient_descent(lr, eps)
    var = init
    grad = gradient(var)

    while abs(var) > eps
        var = var - lr * grad
        grad = gradient(var)

• gradient : 미분계산함수
• init : 초기화 값
• lr : learning rate
  • 미분의 update 속도를 결정
• eps : 학습종료 조건
• var = var - lt * grad 부분이 $x - \lambda f’(x)$를 구현한 부분

2. 다변수 (vector)

Input : gradient, init, lr, eps
Output : var

Algorithm gradient_descent(lr, eps)
    var = init
    grad = gradient(var)

    while norm(var) > eps
        var = var - lr * grad
        grad = gradient(var)

• gradient : gradient($\nabla$) 계산 함수
• 단일변수와 다르게 학습종료 기준은 norm을 계산한 수치로 설정

Gradient Descent By Python

1. 단일변수

\[f(x) = x^2 + 2x + 3 \text{일 때 최소점을 찾는 코드}\]

import sympy as sym
import numpy as np
from sympy.abc import x

def func(val):
    fun = sym.poly(x**2 + 2*x + 3)
    return fun.subs(x, val), fun

def func_gradient(fun, val):
    _, function = fun(val)
    diff = sym.diff(function, x)
    return diff.subs(x, val), diff

def gradient_descent(fun, init, lr=1e-2, eps=1e-5):
    cnt = 0
    val = init
    diff, _ = func_gradient(fun, init)
    
    while np.abs(diff) > eps:
        val = val - lr * diff
        diff, _ = func_gradient(fun, val)
        cnt += 1
    
    print(f"함수 : {fun(val)[1]}, 연산횟수 : {cnt}, 최소점 : ({val}, {fun(val)[0]})")

gradient_descent(fun=func, init=np.random.uniform(-2, 2))

2. 다변수 (벡터)

\[f(x) = x^2 + 2y^2 \text{일 때 최소점을 찾는 코드}\]

import sympy as sym
import numpy as np
from sympy.abc import x, y

def eval_(fun, val):
    val_x, val_y = val
    fun_eval = fun.subs(x, val_x).subs(y, val_y)
    return fun_eval

def func_multi(val):
    x_, y_ = val
    func = sym.poly(x**2 + 2*y**2)
    return eval_(func, [x_, y_]), func

def func_gradient(fun, val):
    x_, y_ = val
    _, function = fun(val)
    diff_x = sym.diff(function, x)
    diff_y = sym.diff(function, y)
    grad_vec = np.array([eval_(diff_x, [x_, y_]), eval_(diff_y, [x_, y_])], dtype=float)
    return grad_vec, [diff_x, diff_y]

def gradient_descent(fun, init, lr=1e-2, eps=1e-5):
    cnt = 0
    val = init
    diff, _ = func_gradient(fun, init)
    
    while np.linalg.norm(diff) > eps:
        val = val - lr * diff
        diff, _ = func_gradient(fun, val)
        cnt += 1
    
    print(f"함수 : {fun(val)[1]}, 연산횟수 : {cnt}, 최소점 : ({val}, {fun(val)[0]})")

pt = [np.random.uniform(-2, 2), np.random.uniform(-2, 2)]
gradient_descent(fun=func_multi, init=pt)