RecSys : Context-aware Recommendation(FM, FFM)
What is Context-aware Recommendation
문제점과 해결책
- 기존의 추천 시스템 방식
- 유저 관련 정보
- 아이템 간련 정보
- 유저-아이템 상호작용
- 기존의 추천 방식은 유저, 아이템의 ID만 사용하는 문제가 있음
- 특히 이런 것은 MF 계열의 CF에서 자주 나타남
- 상호작용의 2차원 행렬 표현 방식
- 유저의 지리, 나이, 성별 특징, 아이템의 카테고리, 태그 등을 넣기에 무리가 있음
- 상호작용을 넣었지만 그 맥락적인 상호작용 정보가 적음이라는 문제 때문에 cold start 문제가 발생
- 이를 해결하고자 컨텍스트 기반 추천 시스템 방법이 제시됨
- 유저-아이템 상호작용 + 맥락 정보를 함께 반영하는 방법
Why Context-aware Recommendataion?
- 실제 서비스에서는 metric 자체보다는 CTR(Click-Through Rate)가 더 현실적인 지표
- 기업의 최종 목표는 유저의 CTR 예측이 핵심
- CTR 예측 방식
- CTR은 결국 클릭의 여부인데, 일반적으로 이진분류로 많이 함
- 하지만 실제 이진 분류보다는 유저의 클릭 확률을 예측하는 것이 더 효율적
- 실제 광고 예측과 같은 유저의 클릭 환경에는 다양한 맥락이 존재함
- 따라서 실제 예측 과정에서 유저 ID는 필요가 없는 경우가 많음
How to CTR Prediction?
\[\text{Logistic Regression} : logit (P(y = 1 \mid x)) = \left( w_0 + \sum_{i=1}^n w_i x_i \right), \quad w_i \in \mathbb{R}\]- 대표적으로 많이 쓰는 로지스틱 회귀 모형
- 여러 feature의 상호작용을 표현하지 못하므로 CTR 예측에 사용하기에는 무리가 있음
- feature 단일의 영향력을 보기에는 충분함
- 변수 간의 상호작용을 표현한 로지스틱 회귀 모형
- 문제는 $x_i$, $x_j$의 수에 맞춰 $w_{ij}$가 나타나는데, 결국 파라미터 수는 $N^2$이 되므로 파라미터 수가 급격하게 증가하는 단점이 존재
데이터의 종류
- Dense Feature
- 벡터로 표현하는 경우 작은 공간에 밀집되는 수치형 변수
- 연속형 변수는 그 자체가 의미를 갖는 경우가 많으므로 수치로 표현해도 충분함
- Sparse Feature
- 벡터로 표현하는 경우 넓은 공간에 있는 범주형 변수
- 범주형 변수도 수치로 임베딩할 수 있지만 이는 수학적으로 의미를 가질 위험이 있음
- 이를 해결하고자 대부분 원핫 인코딩형태로 표현
- 원핫 인코딩 특징상 0으로 표현되는 데이터가 더 많음
- CTR Prediction에서는 대부분 sparse fature가 많음
- Sparse Feature는 말했듯이 아이템의 종류 = feature 수가 되기 때문에 파라미터 수가 과도하게 많아짐
- 이를 해결하고자 Item2Vec, LDA, BERT 등을 활용해서 feature 임베딩을 진행함
Factorization Machine (FM)
Factorization Machines
- Paper: [IEEE 2010] Factorizaion Machines
- SVM과 Factorization Model의 장점을 결합한 모델
문제 제기
- 딥러닝이 등장하기 전에는 Support Vector Machine(SVM) 을 가장 많이 사용함
- SVM의 강점인 커널 공간으로 비선형 데이터 셋에서 강점이 나타남
- SVM의 문제점은…
- CF환경인 Sparse Data 환경이 많은데, SVM은 sparse field에서 취약한 단점을 가짐
- 그런데 CF에 유리한 MF의 문제점은…
- X: (user, item) $\rightarrow$ Y(rating) 같은 특수 환경에서만 가능함
- 비선형 데이터의 처리가 어려움
문제 해결 아이디어
\[\hat{y}(x) = \underbrace{w_0 + \sum_{i=1}^n w_i x_i}_{\text{Logistic term}} + \underbrace{\sum_{i=1}^{n}\sum_{j=i+1}^{n} \langle v_i, v_j \rangle x_i x_j}_{\text{Factorization term}}\] \[w_0 \in \mathbb{R}, \quad w_i \in \mathbb{R}, \quad v_i \in \mathbb{R}^k\]- 논문에서 제시한 모델의 수식은 크게 2개의 항으로 나눠짐
- logistic term은 단일 feature 정보를 학습
- Factorization term은 k차원의 표현과 같은 역할을 함
- Factorization term은 polynomial logistic의 아이디어를 가져왔으나 식이 일부 다른데, weight 역할을 하는 $w_{ij}$가 아닌 dot product를 사용해서 k차원에 대한 더 일반화된 수식을 적용함
- k차원의 경우 factorization dimension인데, 이는 hyperparamter
- 원문 : A row $\mathbf{v}_i$ within $\mathbf{V}$ describes the $i$-th variable with $k$ factors. $k \in \mathbb{N}_0^+$ is a hyperparameter that defines the dimensionality of the factorization.
Sparse 데이터 활용 예측
\[(\text{user}_1, \text{movie}_2, 5) \rightarrow [ \underbrace{1, 0, 0, 0, 0}_{\text{user one-hot}}, \underbrace{0, 1, 0, 0, 0}_{\text{movie one-hot}} ]\]- 평점 데이터 구조는 {(유저 ID, 영화 ID, 평점), …}
- 일반적인 CF 입력과 같음
- 평점 데이터를 일반 입력으로 변화하면 원핫 인코딩 표현으로 변형 (유저 5, 영화 5 인 상황으로 가정)
- 결국 입력 값의 차원은 유저 수 + 아이템 수
- 유저 A의 영화 ST에 대한 평점을 예측하는 경우 아래와 같은 방식으로 학습
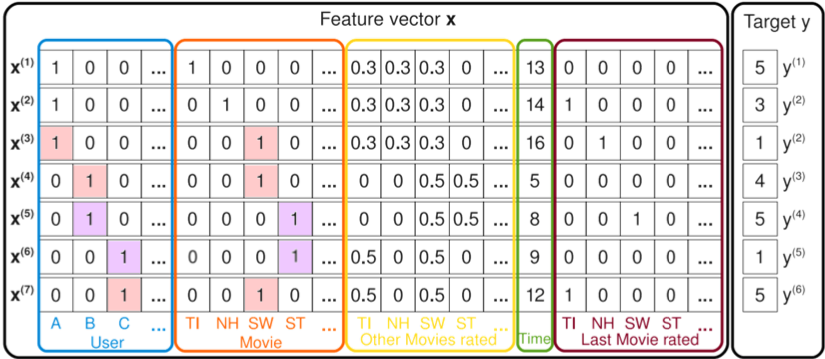Factorization Machines
- $V_{ST}$의 경우 유저 B와 C가 해당 영화를 봤기 때문에 그 유저들이 본 다른 영화 정보를 활용하여 학습
- $V_A$의 경우 A가 본 영화인 SW를 통해 B, C에 대한 정보를 학습
- 그 외에도 뒤쪽에 context를 추가해서 상호작용 정보를 추가로 학습할 수 있음
FM의 장점
- SVM에 비해서…
- sparse data에 취약한 단점을 극복
- 선형 복잡도 $O(kn)$을 갖기 때문에 큰 규모의 데이터도 빠르게 학습함
- 대신 파라미터 수가 선형적으로 비례함
- MF에 비해서…
- 다양한 예측 문제에 사용가능해서 기존에 CF환경에만 가능한 단점을 극복
- 아이템 ID를 제외한 다른 부가 context를 추가로 학습 가능
Field-aware Factorization Machine (FFM)
Fiel-aware Factorization Machine (FFM)
- Paper : Field-aware Factorization Machine
- 기존 FM의 변형을 가한 모델
문제 제기
- FM이 예측 문제라는 범용성을 확대한 상황에서 CTR 예측에 좋은 성능을 보임
- 단, FM의 문제는 사용하는 field의 수가 2개였기 때문에 이를 해결하는 3차원 field 모델인 Pairwise Interaction Tensor Factorization(PITF)가 등장함
- PITF는 (user, item, tage)의 3차원 field 예측을 시도
- (user, item), (user, tag), (item, tag) 쌍을 구성해서 서로 다른 latent factor를 정의
- PITF에서 아이디어를 착안하여 여러 field의 latent factor를 제시
문제 해결 아이디어
\[\hat{y}(x) = w_0 + \sum_{i=1}^n w_i x_i + \underbrace{\sum_{i=1}^{n}\sum_{j=i+1}^{n} \langle v_{i,f_j}, v_{j, f_i} \rangle x_i x_j}_{\text{Factorization term}}\] \[w_0 \in \mathbb{R}, \quad w_i \in \mathbb{R}, \quad v_{i, f} \in \mathbb{R}^k\]- 입력 변수를 필도별로 나누고 필드별로 latent factor를 갖게 factorize 진행
- field는 모델 설계시 정의 같은 의미를 갖는 변수의 집합
- 유저 : 성별, 디바이스, OS
- 아이템 : 광고, 카테고리
- context : 어플리케이션, 배너
- feature 수만큼 필드를 정의할 수 있음
- Factorization term에서 $V_{i, f}$는 $x_i$이 있는 쌍에서 남은 반대 field의 factorize parameter
| Clicked | Publisher(P) | Advertiser(A) | Gender(G) |
|---|---|---|---|
| Yes | ESPN | Nike | Male |
- 위의 상황인 경우 필드는 P, A, G로 정의
- 1개의 변수에 대해 필드의 수($f$)와 factorization 차원($k$)의 곱만큼 학습
- 여기서 factorization dimension은 hyperparameter
- 원문 : A row $\mathbf{v}_i$ within $\mathbf{V}$ describes the $i$-th variable with $k$ factors. $k \in \mathbb{N}_0^+$ is a hyperparameter that defines the dimensionality of the factorization.
FFM field 구성
- 범주형 변수
FM
\[\begin{aligned} &\text{label \; feat:val1 \; fat2:val2 } \cdots, \\ &\rightarrow\qquad \text{YES \; P-ESPN:1 \; A-Nike:1 \; G-Male:1 } \end{aligned}\]FFM
\[\begin{aligned} &\text{label \; field1:feat:val1 \; field2:fat2:val2 } \cdots, \\ &\rightarrow\qquad \text{YES \; P:P-ESPN:1 \; A:A-Nike:1 \; G:G-Male:1 } \end{aligned}\]
- 수치형 변수
- 기존 변수의 encoding과 좀 반대로 수치형 변수를 mapping하는게 복잡하다
- dummy field
- numeric feature 1개 당 한의 필드를 할당
- 수치와 필드가 1:1 매핑 (필드명은 큰 의미가 없음)
- 예시) $\text{ Yes \; AR:AR:45.73 \; Hidx:Hidx:2 \; Cite:Cite:3}$
- discretize
- numeric feature를 n개의 구간으로 나누어 사용
- 논문에서는 소수를 반올림해서 정수로 변환하여 해당 정수 값을 카테고리 변수처럼 다룸
- 예시) $\text{ Yes \; AR:45:1 \; Hidx:2:1 \; Cite:3:1}$
Comments powered by Disqus.