RecSys : Recommender System with Graph Neural Net

Neural Graph Collaborative Filtering의 자세한 내용은 Paper Review 카테고리에 있습니다.

Graph Neural Network

Graph

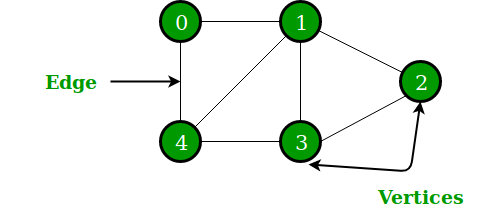
점(node)과 간선(edge)으로 구성된 자료구조
일반적으로 $G = (V, E)$로 정의

Naive Graph Neural Net

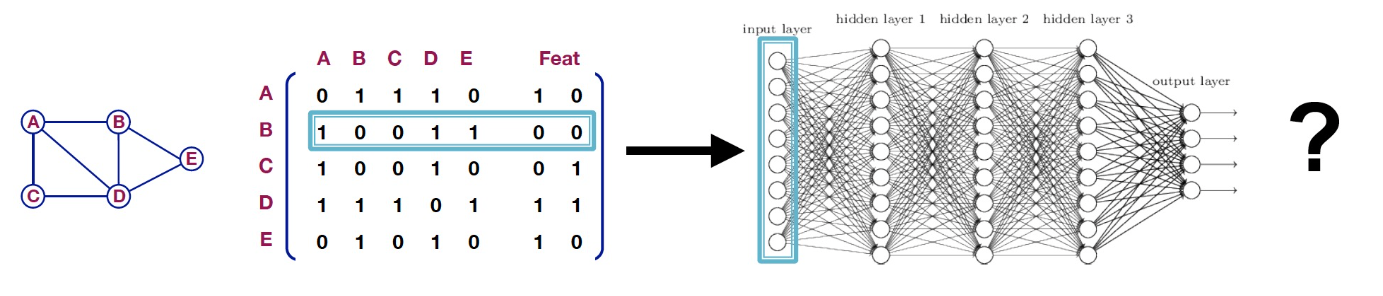
Neural Network에 그래프가 도입된 이유는 크게 2가지
1. 정보간의 관계, 상호작용같은 추상적 개념 표현에 적합
  - 상호작용으로 table로 표현하면 너무 복잡하다는 단점이 있음
  - 추천 시스템에서 유저-아이템 관계를 표현하기에 적합함
2. Non-Euclidean Space 표현이 가능
  - 이미지, 텍스트, tabular는 대부분이 격자 공간에 투영 가능한 euclidean space 데이터
  - SNS데이터, 상호작용, 분자구조는 격자 공간에 투영할 수 없는 non-euclidean space
그래프를 인접행렬 방식으로 표현하여 하나의 노드정보를 MLP에 학습하는 naive approach 방법으로 시작함
문제점
- 노드의 수가 많아지면 인접행렬 그래프 표현의 한계인 연산량 증가문제가 발생함
- 노드의 수만큼 MLP 노드가 추가되므로 모델의 차원 수가 증가하고 결국 모델의 복잡도로 연결됨
- 인접행렬 특성상 표현하는 순서에 따라 의미가 달라지는 경우가 발생

Graph Convolutional Network

Paper : [ICLR 2017] Semi-Supervised Classification with Graph Convolutional Networks

Naive 방식의 문제점을 극복하고자 convolution 연산을 적용한 Graph Convolution Network가 등장
Local Connectivity : 모든 노드를 확인하는 것이 아닌 특정 노드의 주변부를 대상으로 convolution 연산을 진행
Shared Weight : convolution 연산 효과인 주변 노드들과 weight를 공유
multi-layer : convolution을 여러층 쌓으면 떨어져 있는 정보를 확보할 수 있음
- 연산량을 효과적으로 줄이면서 간접적인 관계 파악이 가능

Neural Graph Collaborative Filtering

출처 : ACM2019 Neural Graph Collaborative Filtering

[ACM 2019] Neural Graph Collaborative Filtering
자세한 논문 내용은 논문 리뷰 포스트에 있습니다. 참고 바랍니다.

문제 제기

논문은 기존 CF의 연산 방식의 핵심을 다음과 같이 정의
1. 유저-아이템 임베딩 : latent factor
2. 상호작용의 모델링 : $P^\intercal Q$ (dot product를 통한 선형연산)
기존 CF에는 상호작용 표현의 한계가 존재함
기존 CF의 문제를 interaction function ($P^\intercal Q$)에만 의존하므로 sub-optimal(누락된 부분 정보)한 임베딩을 사용한다고 제시

문제 해결 아이디어

Neural Graph Collaborative Filtering

논문에서 계속 언급하는 Collaborative Signal은 유저-아이템 상호작용(소비관계)을 의미
좌측은 기존 CF방식의 상호작용 표현방식인데, 이 방법은 유저와 아이템 수가 늘어날수록 연결되지 않은 다른 item의 간접적인 상호작용 표현에 한계가 존재함
High-order Connectivity를 사용하면 직/간접적 상호작용을 표시할 수 있음
- GNN을 사용하면 user-item-user 연결관계로 따로 유사도를 계산하지 않아도 user간의 연결관계로 유사도를 파악할 수 있음
- Graph로 관계를 표현하면 $u_1$에 대한 아이템의 추천 강도도 계산할 수 있음
  - $i_4$는 $i_4 \rightarrow u_2 \rightarrow i_2 \rightarrow u_1$ path와 $i_4 \rightarrow u_3 \rightarrow i_3 \rightarrow u_1$ path, 총 2가지 경로로 $u_1$에게 전달됨
  - $i_5$가 $u_1$에게 전달되는 경로는 1개밖에 없으므로 추천 강도는 $i_4 > i_5$가 됨

NGCF 구조

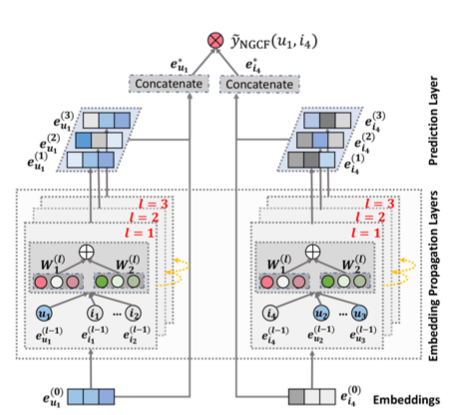Neural Graph Collaborative Filtering

NGCF 모델 구조는 크게 3개의 레이어로 구성됨
- Embedding Layer
  - one-hot encoding의 유저-아이템 초기 임베딩을 k 차원 임베딩으로 변환
- Embedding Propagation Layer
  - NGCF에서 가장 중요한 레이어
  - 유저-아이템 연결관계를 갖는 high-order connectivity를 학습하는 레이어
- Prediction Layer
  - 아이템, 유저 각 전파 레이어에서 전달된 임베딩을 concat해서 결과 score를 연산

Embedding Layer

\[\mathbf{E} = [ \; \underbrace{\mathbf{e}_{u_1}, \cdots, \mathbf{e}_{u_N}}_{\text{users embeddings}} , \underbrace{\mathbf{e}_{i_1}, \cdots, \mathbf{e}_{i_M}}_{\text{item embeddings}} \;]\]

embedding을 생성하는 레이어
임베딩 방식은 기존의 CF방식 (MF, Neural CF)과 동일하지만 기존 CF는 이걸 바로 interaction function에 입력함
NGCF는 GNN에 임베딩을 전파하여 refine
- Collaborative Signal(상호작용)을 직접적으로 레이어에 전달하는 과정

Embedding Propagation Layer

First-order Propagation
- collaborative signal을 전달할 message를 구성하고 결합하는 단계
\[\mathbf{m}_{u\leftarrow i} = f(\mathbf{e}_i, \mathbf{e}_u, p_{ui}) = \frac{1}{\sqrt{ \left\vert\mathcal{N}_{u}\right\vert \left\vert\mathcal{N}_{i}\right\vert }}\left( \mathbf{W}_1\mathbf{e}_i + \mathbf{W}_2 (\mathbf{e}_i \odot \mathbf{e}_u) \right)\]
- Message Construction 단계는 유저-아이템간의 affinity(밀접관계)를 표현하는 message를 형성함
- $p_{ui}$는 연결 item이 과도하게 많을 경우를 방지하는 decay factor
  - 주변 이웃 노드 수($\left\vert \mathcal{N} \right\vert$)로 나눠서 normalize함
\[\mathbf{e}_{u}^{(1)} = \text{LeakyReLU}\left( \mathbf{m}_{u \leftarrow u} + \sum_{i \in \mathcal{N}_{u}} \mathbf{m}_{u \leftarrow i} \right)\]
- Message Aggregation 단계는 $u$의 이웃 노드들에서 전파된 message를 결합하여 해당 유저의 1단(1 layer) 임베딩을 형성함
High-order Propagation
Neural Graph Collaborative Filtering
- $l$개의 embedding propagation layer를 쌓으면 유저노드는 $l$ 거리만큼 떨어진 이웃의 메시지를 사용할 수 있음
  - 이런 이웃들을 $l$-hop neighbor라고 함
\[\mathbf{e}_{u}^{(l)} = \text{LeakyReLU}\left( \mathbf{m}^{(l)}_{u \leftarrow u} + \sum_{i \in \mathcal{N}_{u}} \mathbf{m}^{(l)}_{u \leftarrow i} \right)\] \[\begin{cases} \mathbf{m}^{(l)}_{u\leftarrow i} = p_{ui} \left( \mathbf{W}^{(l)}_1\mathbf{e}^{(l-1)}_i + \mathbf{W}^{(l)}_2 (\mathbf{e}^{(l-1)}_i \odot \mathbf{e}^{(l-1)}_u) \right) \\ \mathbf{m}^{(l)}_{u\leftarrow u} = \mathbf{W}^{(l)}_1\mathbf{e}^{(l-1)}_u \end{cases}\]

Prediction Layer

\[\begin{aligned} \mathbf{e}^{*}_u = \mathbf{e}^{(0)}_u \Vert \cdots \Vert \mathbf{e}^{(L)}_u , \quad \mathbf{e}^{*}_i = \mathbf{e}^{(0)}_i \Vert \cdots \Vert \mathbf{e}^{(L)}_i \\\\ \hat{y}_\text{NGCF}(u, i) = {\mathbf{e}^{*}_u}^\intercal\mathbf{e}^{*}_i \qquad\quad\quad \end{aligned}\]

L번째 layer까지 임베딩 벡터를 형성했으면 user, item 별로 각각 concatenate하여 최종 임베딩 벡터를 생성함
그리고 각 임베딩 벡터를 내적해서 최종 선호도를 계산

LightGCN

GCN의 핵심부분을 가져오고 일부 수정하여 더 가벼운 형태를 제시

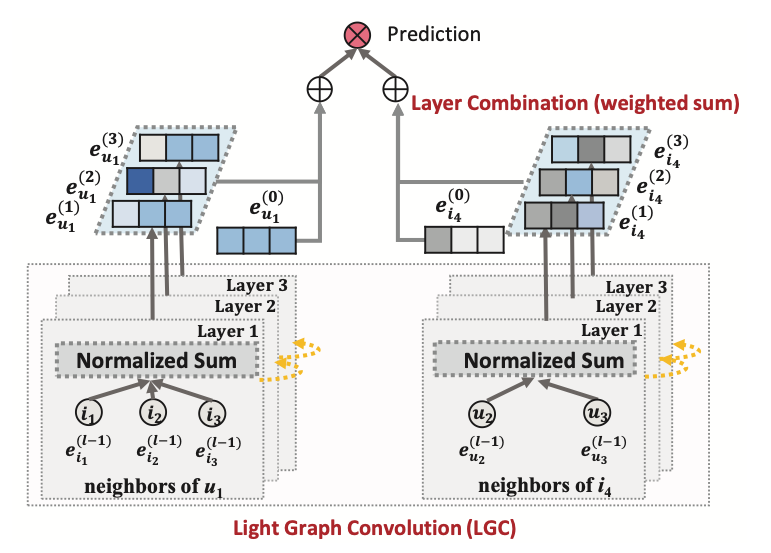LightGCN: Simplifying and Powering Graph Convolution Network for Recommendation

기존 NGCF에서 모든 embedding에 대해 weight parameter를 적용했으나 LightGCN에서는 이웃 노드의 임베딩을 가중합 처리
layer가 깊을수록 멀리있는 정보이므로 강도가 약할 것이라는 아이디어를 사용함

\[\mathbf{e}^{(k+1)}_u = \sum_{i\in\mathcal{N}_u}\frac{1}{\sqrt{\lvert \mathcal{N}_u \rvert}\sqrt{\lvert \mathcal{N}_i \rvert}}\mathbf{e}^{(k)}_i\]

주변에 연결되어 있는 노드만 사용하므로 self-connection 항이 제거됨
실제 학습 파라미터는 0번째 임베딩 레이어에만 존재함
one-hot encoding이 embedding으로 표현되는 부분에서만 weight가 존재함

\[\mathbf{e}_u = \sum_{k=0}^{K}\alpha_k\mathbf{e}^{(k)}_u\]

최종 예측에서도 k층 레이어의 임베딩에 가중치 $\alpha$를 곱해서 가중합 처리를 함
이때, $\alpha_k = (k+1)^{-1}$로 설정해서 레이어가 깊을수록 가중치가 0에 가까워져서 영향력을 낮추게함

[BoostCamp AI Tech / RecSys] Day36 - RecSys with GNN