RecSys : Matrix Factorization

강의에서는 ALS와 BPR을 다뤘지만 두 내용은 논문을 직접 읽고 분석할 예정이므로 Paper Review 카테고리에 업데이트 될 예정입니다.

Model Based CF

이전에 언급한 Neighborhood-Based CF는 Sparsity와 Scalability 문제가 존재했음
NBCF는 데이터를 메모리에 올려놓고 사용한다고해서 Memory-based CF라고도 함
이 문제를 해결하고자 모델 기반 협업 필터링(MBCF) 이 등장함
단순히 유사도를 비교하는 것보다 데이터 내부의 패턴분석을 통해 추천하는 방식
Parametric Machine Learning 방식
데이터 정보가 파라미터(데이터 패턴)로 모델에 적용되고 이 파라미터를 학습하는 것이 목표
장점
- 모델을 학습하여 압축된 형태로 저장함
- 기존 모델 서빙처럼 학습된 모델을 통해 추천하므로 서빙 속도가 빠흠
- NBCF의 문제인 sparsity, scalability 한계 극복
  - Sparsity Ratio가 99.5%가 넘어도 좋은 성능을 보임
- NBCF는 특정 K개의 이웃에 대해 추천하므로 오버피팅의 위험이 존재하지만 MBCF는 모든 데이터 패턴을 학습하므로 이를 방지할 수 있음
- NBCF는 이론적으로는 그럴듯하지만 현실의 데이터에서는 일정 기준치를 넘는 유사도를 갖는 케이스를 찾기가 어려운 문제가 존재함 (Limited coverage)

NBCF VS MBCF

NBCF는 특정 무언가를 학습하는 것이 아닌 단순 저장된 데이터를 통해 계산하는 방식으로 추천
MBCF에서 등장하는 유저, 아이템 벡터는 모두 학습 과정을 통해 업데이트하는 파라미터

Feedback

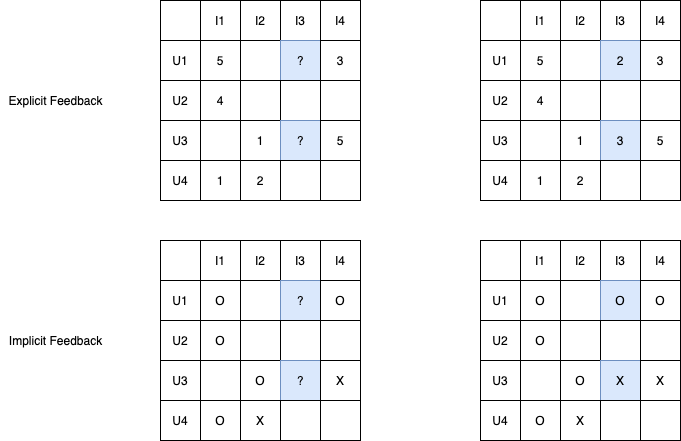
Explicit Feedback

영화 평점, 별점 등 유저가 아이템에 대한 직접적인 선호 강도를 표현한 데이터
데이터 추천에 있어서 가장 편리한 수단

Implicit Feedback

클릭 여부, 시청 여부, 페이지 접속 등 아이템에 대한 유저의 간접적인 선호를 표현한 데이터
상호작용의 여부이므로 일반적으로는 binary 형태로 기록
현실적으로 가장 많이 존재하는 데이터

Latent Factor Model

Latent Factor Model이란 최근에는 Embedding이라고 부름
유저와 아이템의 관계는 매우 복잡한 요소들로 이루어져 있으나 이를 간단한 몇 개의 벡터 차원으로 embedding할 수 있다는 모델 컨셉
유저-아이템 행렬을 저차원 행렬로 분해하는 방법으로 작동
- black box인 모델 특성상 latent factor가 어떤 패턴을 추출한지는 알 수 없음
핵심 아이디어는 유저와 아이템을 동일 벡터공간에 두고 유저와 아이템의 유사도를 동시에 판단

SVD : Singular Value Decomposition

\[R = U \Sigma V^{\intercal}\]

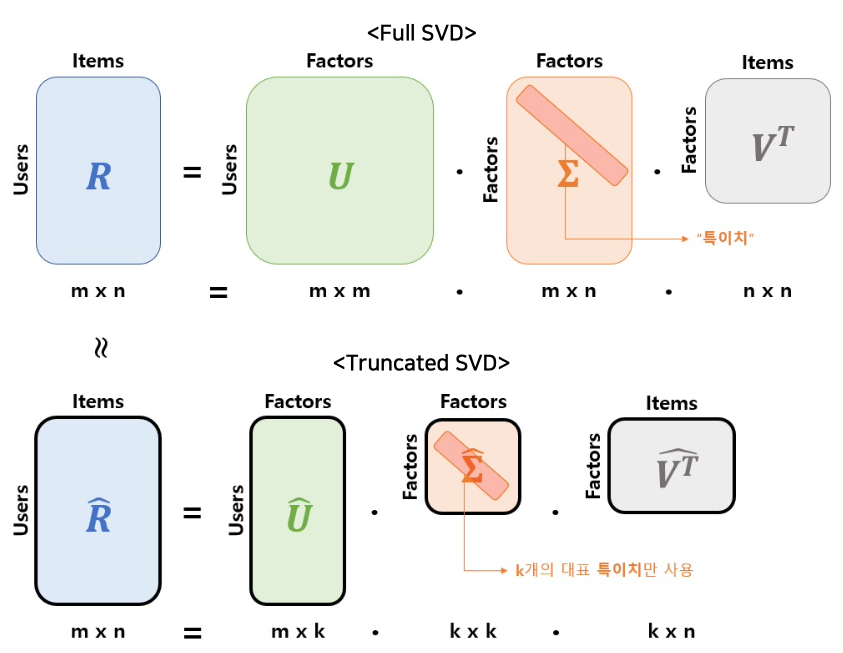
SVD는 선형 대수학에서 차원 축소 기법 중 하나
유저가 책정한 rating이 담겨있는 rating matrix($R$)를 3개의 벡터로 분해
- $U$ : 유저-잠재 행렬 (user-latent matrix)
- $\Sigma$ : 잠재 대각행렬 (latent matrix)
  - $RR^\intercal$을 고유값 분해하여 나오는 값
- $V$ : 아이템-잠재 행렬 (item-latent matrix)
모든 latent factor를 사용하는 것보다 가장 중요한 정보들만 살려서 연산을 하는 Truncated SVD를 사용하기도 함
정확하게 $R$로 복원할 수는 없지만 유사하고 근접한 $\widehat{R}$로 복원
한계점
- SVD는 non-sparse matrix에 한해서만 연산이 가능
  - 하지만 현실 데이터는 sparse matrix
  - 이를 해결하고자 결측치를 채우는 과정에서 데이터의 왜곡과 연산비용이 증가
SVD의 한계를 해결하고자 Matrix Factorization이 등장

Matrix Factorization

User-Item 행렬을 저차원의 User와 Item의 latent factor 행렬의 곱으로 분해하는 SVD 방식 개념을 활용
관측된 데이터만 활용할 수 있게 SVD를 변형하여 활용
Rating Matrix를 $P$와 $Q$로 분해하여 가장 유사한 $\widehat{R}$을 추론

MF 기본 원리

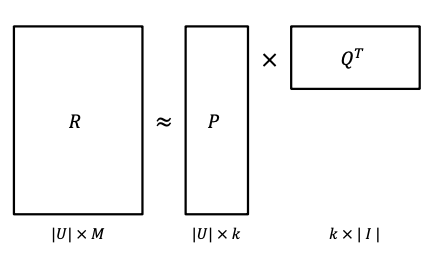
\[\underset{P,Q}{\min} \sum_{\text{observed } r_{u,i}} (r_{u,i} - p_{u}^\intercal q_{i})^2\]

실제 rating matrix ($R$)과 유사한 rating matrix인 ($\widehat{R}$)의 오차가 최소가 되게 하는 것이 목적
실제 코드 구현에서는 마치 layer의 초기 weight가 랜덤으로 초기화된 것처럼 무작위의 형태로 $P$와 $Q$를 설정
- 구현적인 부분은 따로 포스팅을 할 예정
MF의 핵심적인 요소들을 알아보면서 원리를 깊게 알아보겠다.

Objective Function

\[\underset{P,Q}{\min} \sum_{\text{observed } r_{u,i}} (r_{u,i} - p_{u}^\intercal q_{i})^2 + \lambda(\lVert p_{u}\rVert_2^2 + \lVert q_{i} \rVert_2^2)\]

모델 학습에 사용되는 목적함수는 위의 식으로 구성되어 있음
2가지 항으로 구성
- $\underset{P,Q}{\min} \sum_{\text{observed } r_{u,i}} (r_{u,i} - p_{u}^\intercal q_{i})^2$ : 실제 목적함수
- $\lambda(\lVert p_{u}\rVert_2^2 + \lVert q_{i} \rVert_2^2)$ : Regularization 항
$p_u$, $q_i$는 유저와 아이템의 latent vector이고 목적함수를 통해 지속적으로 업데이트되는 matrix 형태의 파라미터
- 여기서 잘 생각해보면 이전에 언급한 matrix가 선형 대수학에서 어떤 의미인지와 연관성이 깊다고 볼 수도 있다.
- 우리가 모델에 layer를 쌓는 것은 weight matrix를 곱하여 vector space를 변화해주는 역할이었다.
- 물론 이렇게 vector space를 변화해주는 것인지는 확실치 않지만 결국 layer를 쌓은 것처럼 weight가 담긴 matrix의 weight를 학습하는 것과 유사한 원리이다.
뒤쪽의 항은 L2-regularization인 규제항
- 규제항의 역할은 학습 데이터의 과적합을 방지해주는 역할

Regularization

\[\lambda(\lVert p_{u}\rVert_2^2 + \lVert q_{i} \rVert_2^2)\]

weight를 loss function에 넣어주면 weight가 너무 커지지 않도록 제한이 걸려서 overfitting이 되는 것을 방지함
$\lambda$는 일반적으로 하이퍼파라미터로 결정되며 영향력을 결정함

SGD

\[\begin{aligned} \text{Loss: } L = \sum (r_{u,i}-p_u^\intercal q_i)^2 + \lambda(\lVert p_{u}\rVert_2^2 + \lVert q_{i} \rVert_2^2) \end{aligned}\]

Original MF의 아이디어에서는 SGD를 통해 모델 파라미터를 학습
Loss function은 앞서 설명한 목적함수를 활용해서 계산

\[\text{Gradient: } \frac{\partial L}{\partial p_u} = \frac{\partial (r_{ui}-p_t^\intercal q_i)^2}{\partial p_u} + \frac{\partial \lambda \lVert p_{u}\rVert_2^2}{\partial p_u}\]

$p_u$와 $q_i$에 대해 각각 gradient를 계산해서 update 진행

\[\begin{aligned} \text{Error: } e_{ui} = r_{ui} - p_u^\intercal q_i \qquad\qquad\qquad\qquad \\\\ \text{Gradient} = -2(r_{ui} - p_u^\intercal q_i)q_i + 2\lambda p_u = -2(e_{ui}q_i - \lambda p_u) \end{aligned}\]

기존의 gradient update와 동일한 방식을 사용해서 반대방향으로 $p_u$, $q_i$ 업데이트

\[\begin{aligned} p_u \leftarrow p_u + \eta\cdot(e_{ui}q_i - \lambda p_u)\\ q_i \leftarrow q_i + \eta\cdot(e_{ui}p_u - \lambda q_i) \end{aligned}\]

-2는 원래 적는게 맞지만 그냥 learning rate에 포함된 계산이라 생략된다.

Matrix Factorization Techniques for Recommender Systems

Netflix Prize 대회 우승 논문으로 대표적인 MF 추천 논문
오리지널 MF에 추가적인 테크닉을 적용하여 성능을 향상함
핵심은 다른 것을 수정하는 것이 아닌 목적함수를 수정

Adding Biases

\[\underset{P,Q}{\min} \sum_{\text{observed } r_{u,i}} (r_{u,i} - {\color{red}{\mu - b_u - b_i}} - p_{u}^\intercal q_{i})^2 + \lambda(\lVert p_{u}\rVert_2^2 + \lVert q_{i} \rVert_2^2 + {\color{red}{b_u^2 + b_i^2}})\]

위에서 언급한 유저별로 평점의 분포가 다를 수 있다는 것을 고려한 편차를 적용하는 방법을 도입
전체 평균($\mu$), 유저/아이템의 bias를 추가해서 이를 보정하는 새로운 목적함수를 설정
에러도 이에 맞춰 수정
$e_{ui} = r_{ui} - \mu - b_u - b_i - p_u^\intercal q_i$

\[\begin{aligned} & b_u \leftarrow b_u + \gamma\cdot(e_{ui} - \lambda b_u) \\ & b_i \leftarrow b_i + \gamma\cdot(e_{ui} - \lambda b_i) \\ & p_u \leftarrow p_u + \gamma\cdot(e_{ui}q_i - \lambda p_u) \\ & q_i \leftarrow q_i + \gamma\cdot(e_{ui}p_u - \lambda q_i) \\ \end{aligned}\]

항이 늘어난만큼 추가적인 gradient update도 진행 $\gamma$는 learning rate

Adding Confidence Level

\[\underset{P,Q}{\min} \sum_{\text{observed } r_{u,i}} {\color{red}{c_{u,i}}}(r_{u,i} - {\mu - b_u - b_i} - p_{u}^\intercal q_{i})^2 + \lambda(\lVert p_{u}\rVert_2^2 + \lVert q_{i} \rVert_2^2 + {b_u^2 + b_i^2})\]

모든 평점 데이터가 동일한 신뢰도를 갖지 않는다는 문제를 보완
- 특정 아이템이 많이 노출되어 클릭률이 높은 경우
- 유저가 정확한 평점을 입력하지 않은 경우
각 rating에 대한 신뢰도인 $c_{u,i}$를 추가

Adding Temporal Dynamics

\[\begin{aligned} \widehat{r_{ui}(t)} = \mu + b_u(t)+b_i(t)+p_u^\intercal q_i(t) \\\\ b_u(t) = b_u + \alpha_u\cdot sign(t - t_u)\cdot |t-t_u|^\beta \end{aligned}\]

아이템은 시간이 흐름에 따라 인기도가 떨어지는 경향이 있음
유저는 새로운 아이템에 더 긍정적이고 오래된 아이템에 부정적인 경향이 나타나는 엄격해지는 경향성을 보임
이러한 시간의 흐름을 반영하는 모델을 설계

[BoostCamp AI Tech / RecSys] Day34 - Matrix Factorization