[BoostCamp AI Tech / RecSys] Day32 - Content Based Recommendation

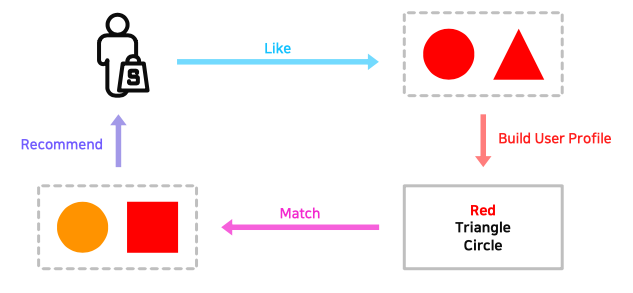
RecSys : Content Based Recommendation

---

Content-based Recommendation

• 유저가 과거에 선호한 아이템을 기반으로 비슷한 아이템을 유저에게 추천
• 장점
  • 다른 유저의 데이터가 필요하지 않으므로 서비스 초반에 활용하기 좋음
  • 새로운 아이템 또는 인기도가 낮은 아이템 추천 가능 (long-tail problem 극복가능)
  • 추천 아이템이 explainable해짐 $\rightarrow$ 아이템의 특성이 곧 추천의 이유
• 단점
  • 아이템의 적합한 feature를 찾기 어려움
  • 특정 concept의 추천 결과만 나올 수 있음 (overspecialization)
  • 다른 유저의 데이터를 활용할 수 없음

---

Item Profile

• 추천을 위해서는 item의 특성을 활용하므로 item의 feature로 구성된 profile을 만들어야 함
• 각 item의 특성을 살리는 것이 중요 (ex. 영화 장르, 음악 장르 등…)
• 일반적으로 아이템 feature는 vector로 표현

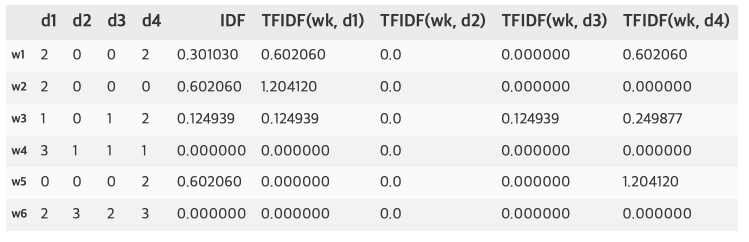
TF-IDF

\[\begin{aligned} TF(w, d) = freq_{w,d}\quad \text{ or }\quad \frac{freq_{w, d}}{\underset{k}{max}(freq_{k,d})}\qquad\qquad \\ IDF(w) = \log\frac{N}{n_w} \quad \text{(N: 전체 문서 수, n_w: w가 등장한 문서 수)} \end{aligned}\] \[TF-IDF(w,d) = TF(w,d) \cdot IDF(w)\]

• TF는 단어 w가 문서 d에 등장하는 횟수
  • TF의 경우 특정 단어w가 문서 d에 얼마나 많이 등장하는가? 를 의미
• IDF는 전체 문서 중 단어 w가 등장한 비율의 역수
  • 단순히 TF만 처리를 하면 영어는 is, a, the 같은 관사나 be동사가 극단적으로 많이 나타나고, 한국어는 조사가 많이 등장하는 문제가 발생
  • 이를 해결하고자 IDF를 도입하는데, IDF는 특정 단어 w가 전체 문서 D에서 얼마나 적게 등장하는가? 를 의미함
  • smoothing을 위해 log 연산 처리
• TF-IDF의 연산 특성상 단어 w가 문서 d에서는 많이 등장하면서 전체 문서 D에서는 적게 나타날수록 곱연산의 값이 커지게 됨
  $\rightarrow$ 단어 w가 특정 문서 d를 잘 표현한다고 볼 수 있음

• 대략적으로 d1에 대한 각 단어들의 TF-IDF를 계산하면 이 값은 d1의 vector
  $\rightarrow v_{d1}=(0.6, 1.2, 0.12, 0, 0, 0)$

---

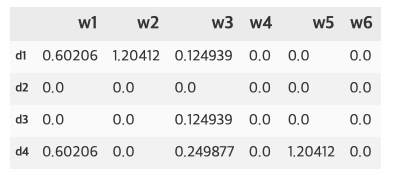
User Profile 기반 추천

• item profile이 모두 구축되었다면 user profile을 구축해서 유저의 선호 리스트를 파악해야함
• 각 유저의 과저 item list의 item vector들을 통합하면 user profile이 됨
  • 단순한 방법 : item vector의 평균계산
  • 유저의 평점이 존재하면 평점을 가중치로 정규화한 평균을 활용
• 만약 위의 item profile에서 유저가 d1과 d3를 선택하였고 rating이 각각 3, 5로 평가했다고 하면 다음과 같이 user profile을 생성 가능

\[\begin{aligned} \text{simple vector} = \frac{v_{d1}+v_{d3}}{2} \quad\quad \\ \text{variant vector} = \frac{r_{d1}v_{d1} + r_{d3}v_{d3}}{r_{d1}+r_{d3}} \end{aligned}\]

• 이렇게 구한 User profile과 item vector 간의 유사도를 분석해서 item을 추천함

Cosine Similarity

\[\cos(\theta) = \cos(X, Y) = \frac{X \cdot Y}{|X| |Y|} = \frac{\sum_{i=1}^{N} X_iY_i}{\sqrt{\sum_{i=1}^{N} X_{i}^2} \sqrt{\sum_{i=1}^{N}Y_i^2}}\]

• 두 벡터의 내적원리를 이용하여 두 벡터의 cos 거리를 계산함
• cosine 함수의 성질에 따라 두 벡터의 방향이 같을수록 1에 가깝고 다를수록 -1에 가까움
• 이를 활용하여 user와 item의 점수를 환산해서 아이템을 추천

\[score(u, i) = \cos(u, i) = \frac{u \cdot i}{|u| \cdot |i|}\]

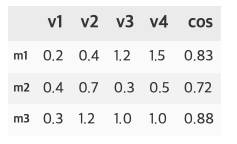
User Rating 예측

\[\begin{aligned} sim(i, i') = \cos(v_i, v_{i'}) \qquad\quad \\ prediction(i') = \frac{\sum_{i=1}^{N} sim(i, i')\cdot r_{u,i}}{\sum_{i=1}^{N} sim(i, i')} \end{aligned}\]

• 새로운 아이템 $i’$이 주어졌을 때 해당 아이템의 평점을 예측할 수 있음
• variant vector와 유사하게 유저가 매긴 평점이 가중치로 들어간 가중평균처리가 됨

• 이 경우 m4 = (0.4, 1.4, 3.1, 1.0)인 새로운 아이템이 도입될 경우 유사도를 구한 것이다.
• 각 아이템은 (3.0, 2.5, 4.0)으로 평점을 유저가 준 경우 새로운 아이템 m4의 예측 평점은 다음과 같다.

def cal_cosine(x, new):
    val1 = np.dot(x, new)
    val2 = norm(x) * norm(new)
    return round(val1/val2, 2)

data = {
    "v1":[0.2, 0.4, 0.3],
    "v2":[0.4, 0.7, 1.2],
    "v3":[1.2, 0.3, 1.0],
    "v4":[1.5, 0.5, 1.0],
}

df = pd.DataFrame(data, index=['m1', 'm2', 'm3'])
m4 = np.array([0.4, 1.4, 3.1, 1.0])
df['cos'] = df.apply(lambda x: cal_cosine(x, m4), axis=1)

sim = df['cos'].values
rating = np.array([3.0, 2.5, 4.0])

print(f"M4's rating: {((sim@rating)/np.sum(sim))}")