RecSys : 추천 시스템 평가 지표와 인기도 추천
추천 시스템의 목표
- 추천 시스템의 목표는 유저에게 필요한 아이템을 추천하는 것
- 이를 위해서는 유저와 관련된 아이템들의 랭킹을 산정하거나 아이템 선택을 예측할 필요가 있음
- 어떤 케이스의 문제를 처리하느냐에 따라 사용하는 평가 지표가 다름
- 추천 모델의 성능 평가는 단순히 모델적 지표만 사용하기엔 무리가 있기 때문에 비즈니스/서비스적 관점의 지표를 더 중요하게 확인함
- 매출, PV(Page View)증가
- 유저의 CTR(Click Through Rate) 상승
- 품질적인 관점의 지표도 많이 고려함
- 연관성 : 추천 아이템과 유저의 연관성
- 다양성 : Top-K의 아이템이 얼마나 다양한 아이템인가?
- 새로움 : 얼마나 새로운 아이템이 추천되는가? (반복적인 아이템 추천은 유저 만족도 감소)
- 참신함 : 유저가 생각하지 못하거나 기대하지 않은 뜻밖의 아이템이 추천되는가? (연관성과 상충되는 요소가 있을 수 있음)
오프라인 테스트
- 오프라인 테스트(Offline Test)는 새로운 추천 모델을 검증할 때 가장 우선적으로 수행되는 단계
- 수집 데이터를 train/valid/test로 나누어 성능 지표 판단
- offline test에서 좋은 성능을 보여야 서빙에 투입되지만 실제 서비스에서는 다양한 상황이 나타나는 serving bias가 발생
- 랭킹과 예측문제에 따라 평가 지표가 다름
랭킹 문제
Precision / Recall @K
\[\begin{aligned} \text{Precision@K} = \frac{\text{# of user preferred items in recom list}}{K} \\ \text{Recall@K} = \frac{\text{# of user preferred items in recom list}}{\text{# of total user preferred items}} \end{aligned}\]- Precision@K : 추천한 K개 아이템 중 실제 유저가 관심있는 아이템의 비율
- Recall@K : 유저가 관심있는 전체 아이템 중 추천한 아이템의 비율
Mean Average Precision(MAP)@K
\[\begin{aligned} \text{AP@K} = \frac{1}{m}\sum_{i=1}^{K}\text{Precision@}i \\ \text{MAP@K} = \frac{1}{|U|}\sum_{u=1}^{|U|}(\text{AP@K})_{u} \end{aligned}\]- AP@K는 Precision@1부터 Precision@K까지의 평균값
- 관련 아이템을 더 높은 순위에 추천할수록 점수 상승
- MAP@K는 모든 유저에 대한 AP@K를 평균한 것
- AP@K는 Precision@1부터 Precision@K까지의 평균값
Normalized Discounted Cumulative Gain(NDCG)
\[\begin{aligned} \text{CG}_{K} = \sum_{i=1}^{K} rel_{i} \qquad \\ \text{DCG}_{K} = \sum_{i=1}^{K}\frac{rel_i}{\log_2(i+1)} \\ \text{IDCG} = \sum_{i=1}^{K}\frac{rel_{i}^\text{opt}}{\log_{2}{(i+1)}} \\ \text{NDCG} = \frac{\text{DCG}}{\text{IDCG}} \qquad \end{aligned}\]- Cumulative Gain (CG) : 상위 K개 아이템에 대한 관련도를 합한 것 순서에 따른 discount는 적용하지 않음
- Discounted CG (DCG) : 순서에 따라 CG를 discount
- Idea DCG (IDCG) : 이상적인 추천이 발생했을 시 DCG값, 가능한 DCG 중 제일 큰 값
- Normalized DCG (NDCG) : 추천 결과에 따라 구해진 DCG를 IDCG로 나눈 값
Online A/B Test
- offline test에서 검증된 가설이나 모델을 이용해서 실제 추천 결과를 서빙하는 단계
- 적용 전후를 비교하는 것이 아닌 동시에 비교군과 대조군을 적용해서 성능을 평가
- 측정하고자하는 부분 제외하고 다른 환경은 최대한 동일하게 유지해야함
- 현업에서는 결국 의사결정시 모델 성능보다 매출, CTR등 비즈니스/서비스 지표를 활용함
인기도 기반 추천 시스템
- 이름 그대로 인기있는 아이템을 추천
- 인기도의 척도는 갖고있는 아이템이 무엇인가에 따라 결정됨
- 인기도 척도를 선정하는 과정에선 다음을 고려
- Most Popular (많은 조회수)
- Highly Rated (높은 평점)
- Recently (최신성)
- 뉴스와 같은 경우 가장 중요한 것은 최신성이므로 최신 정보를 잘 처리하는 것이 좋음
Hacker News Fromula
\[score = \frac{pageviews - 1}{(age+2)^{gravity}}\]- 뉴스는 많은 조회와 최신 정보라는 2가지가 모두 고려되어서 추천해야 함
- 기본적으로 오래된 뉴스는 높은 조회수를 기록할 수 밖에 없으므로 이를 고려해서 시간을 discount하는 요소로 활용해야 함
- 시간에 따라 줄어들게 score를 조정하고자
gravity상수를 사용
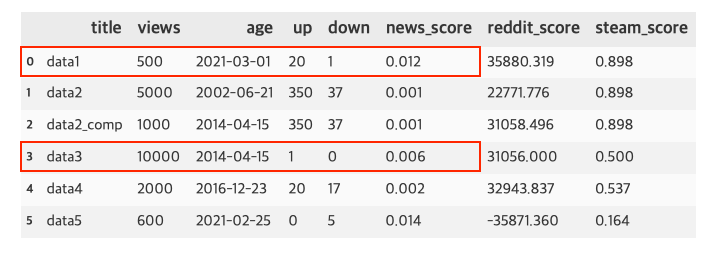
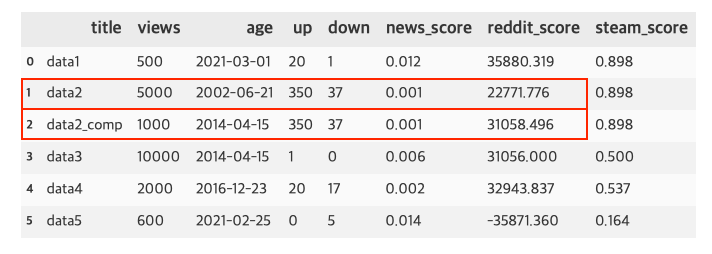
Reddit Formula
\[score = \log_{10}(\max(ups - downs, 1)) + \frac{sign(ups-downs)\cdot seconds}{45000}\]- 실제 reddit에서 사용하는 포스트 스코어
- 2개의 term으로 이루어진 공식으로 첫번째 term은 popularity, 두번째 term은 포스팅 게시된 절대 시간
- 나중에 게시된 포스팅일수록 절대시간이 크므로 높은 score를 가짐
- 첫항의 log term에 의해 초반부 vote가 높은 가치를 갖게됨
- 오래된 포스트일수록 아주 많은 vote가 있어야 높은 score가 생성
- 첫항에서 down vote가 더 많을 때를 방지하고자 down vote가 더 많으면 1로 세팅
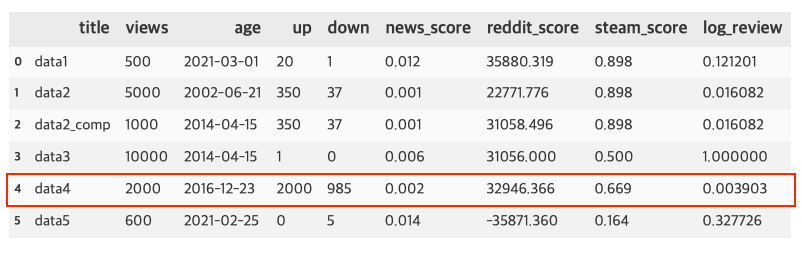
Steam Rating Formula
\[\begin{aligned} \text{avg_rating} = \frac{\text{# of positive reviews}}{\text{# of reviews}} \qquad\qquad \\ score = \text{avg_rating}-(\text{avg_rating - 0.5})\cdot 2^{-\log(\text{# of reviews})} \end{aligned}\]- rating의 평균치를 사용하되, 전체 review 수에 맞춰 rating 보정
- review가 너무 적으면 평균 rating에서 수치를 보정함
- review 개수가 많을 경우 $2^{\log}$ 항이 0에 가까워지므로 보정값의 영향이 없어져서 평균 rating과 유사해짐

Comments powered by Disqus.