DL Basic : Recurrent Neural Networks

Sequential Model

sequential model의 특징은 받아들여야 할 data의 dimension을 모름

Naive sequence model

\[p(x_t | x_{t-1}, x_{t-2}, \cdots)\]

과거에 있는 모든 정보를 고려함
고려해야할 정보량이 점차 증가함

Autogressive model

\[p(x_{t} | x_{t-1}, \cdots, x_{t-\tau})\]

naive 모델의 조건부 데이터의 양이 너무 많아서 과거의 데이터 일부만 고려
AR모델은 과거의 데이터 몇개를 참고하냐에 따라 이름이 바뀜

Markov model (firts-order autoregressive model)

\[p(x_{1}, \cdots, x_{T}) = p(x_{T}|x_{T-1})p(x_{T-1}|x_{T-2})\cdots p(x_2|x_1)p(x_1) = \prod_{t=1}^{T}p(x_{t}|x_{t-1})\]

Morkov assumption을 활용한 모델
AR모델에서 1개의 이전 데이터까지만 참고함
데이터의 가정으로는 말이 되긴 어려움
- 오늘 일어나는 일은 어제의 일에만 영향을 받는다.

Latent autoregressive model

\[\begin{aligned} & \hat{x} = p(x_{t}|h_{t}) \\ & h_t{} = g(h_{t-1}, x_{t-1}) \end{aligned}\]

과거 정보들을 한번에 사용하는 것은 어려움
과거 정보들을 요약해주는 $h_n$을 다음 $h_{n+1}$로 전달

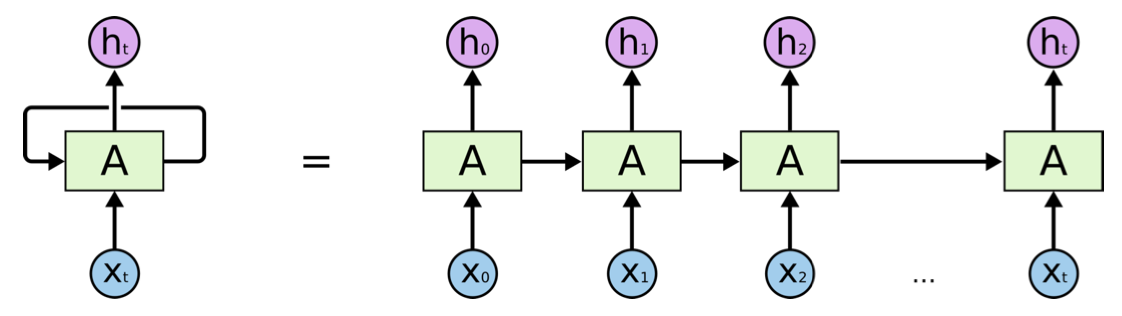
Recurrent Neural Network (RNN)

기본적인 구조는 MLP와 동일함
hidden layer인 $h_{t}$는 이전 cell state에 의존함
대체로 왼쪽 그림처럼 표현하지만 시간순으로 펼치면 우측처럼 나타남

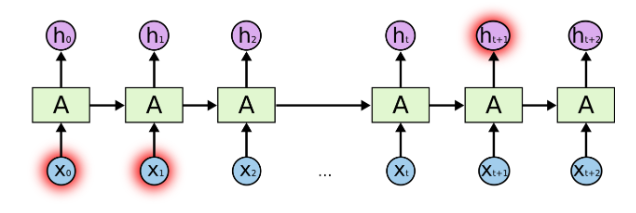
RNN의 문제점

RNN은 연속적인 Backpropagation 때문에 과거로 갈수록 데이터의 영향력이 줄어드는 장기 의존성 (short-term dependencies)문제를 갖는다.

\[\begin{aligned} & h_{1} = \phi(W^\intercal h_0 + U^\intercal x_1) \\ & h_{2} = \phi(W^\intercal \phi(W^\intercal h_0 + U^\intercal x_1) + U^\intercal x_2) \\ & h_{3} = \phi(W^\intercal \phi(W^\intercal \phi(W^\intercal h_0 + U^\intercal x_1) + U^\intercal x_2) + U^\intercal x_3) \end{aligned}\]

위 수식과정에서 계속해서 weight가 곱해지면 vanishing gradient나 exploding gradient가 발생

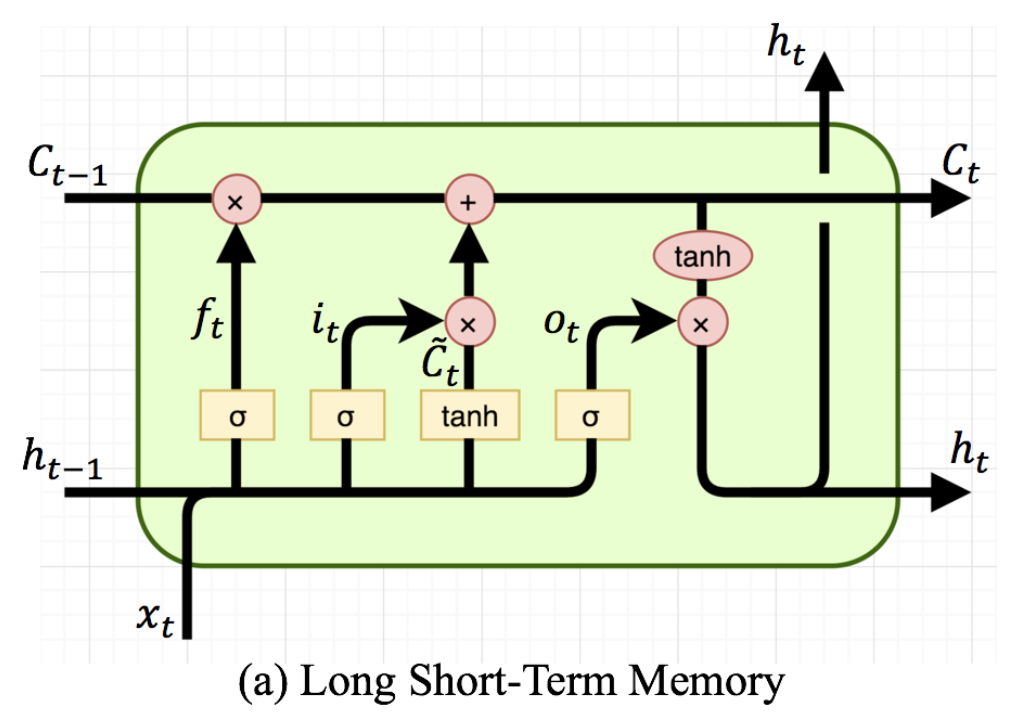
Long Shot Term Memory (LSTM)

LSTM은 Vanila RNN의 단점인 장기 의존성 문제를 해결
왼쪽부터 각 $\sigma$들은 Forget gate, Input gate, Output gate를 의미
이전 cell state ($C_{t-1}$)와 이전의 hiddne state($h_{t-1}$)를 그대로 받아옴
기본 아이디어는 $C_{t-1}$에 각 gate를 통과한 정보들이 $C_{t-1}$ 정보를 업데이트

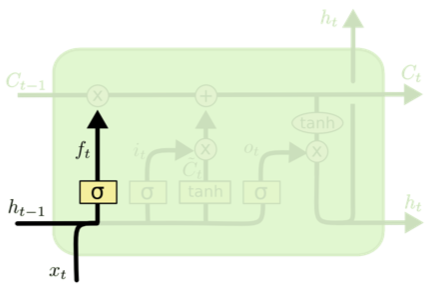
Forget Gate

\[0 \leq f_{t} = \sigma(W_{f}\cdot [h_{t-1}, x_{t}] + b_{f}) \leq 1\]

이전 cell state에서 버릴 것들을 선택

Input Gate

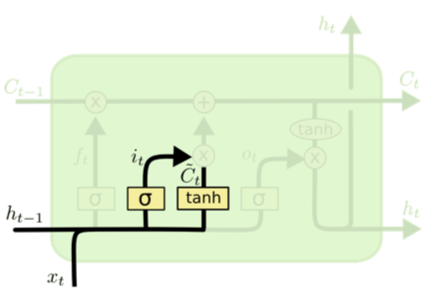
\[\begin{aligned} & i_{t} = \sigma(W_i\cdot [h_{t-1}, x_t] + b_i) \\ & \tilde{C}_{t} = \tanh(W_{C}\cdot[h_{t-1}, x_{t} + b_{C}]) \end{aligned}\]

앞으로 새로 들어오는 정보 중 어떤 것을 새롭게 올릴지를 결정($i_t$)
$\tanh$이 새로운 후보값들인 $\tilde{C}_{t}$ vector를 생성하고 cell state에 더할 준비를 함

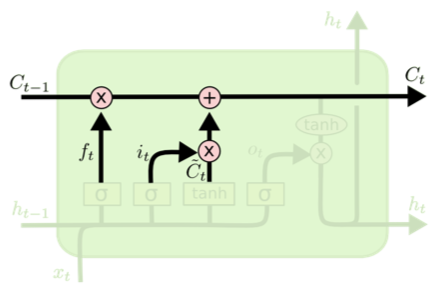
Update Cell

\[\begin{aligned} & i_{t} = \sigma(W_{i} \cdot [h_{t-1}, x_{t}] + b_{i}) \\ & C_{t} = f_t * c_{t-1} + i_{t} * \tilde{C}_{t} \end{aligned}\]

이전 state에 $f_{t}$를 곱해서 잊어버리기로 한 데이터르 잊음
$i_t$를 통해 어떤 데이터가 들어갈지 선택하고 $\tilde{C}_t$를 곱한 input gate 결과를 합해서 새로운 cell state를 형성

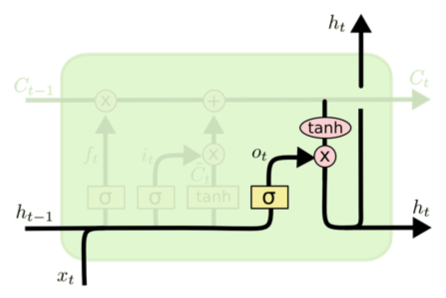
Output Gate

\[\begin{aligned} & o_{t} = \sigma(W_{o} [h_{t-1}, x_t] + b_{o}) \\ & h_t = o_t * \tanh(C_t) \end{aligned}\]

어떤 값을 내보낼지 결정함
시그모이드를 통해 원하는 output을 결정함

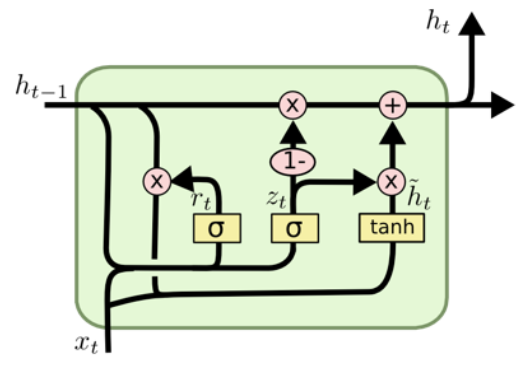
Gated Recurrent Unit (GRU)

LSTM의 변형 모델
peephole connection을 추가하였고 일부 게이트를 변형함
reset gete, update gate가 존재
cell state는 없고 hidden state만 존재
LSTM보다 파라미터 수가 적어서 더 성능이 좋음

[BoostCamp AI Tech / Level 1 - DL Basic] Day16 - Recurrent Neural Networks