[BoostCamp AI Tech / Level 1 - DL Basic] Day14 - Generative Models

DL Basic : Generative Models

---

주의! 열심히 노력했으나 어려워서 틀린 내용이 있을 수 있습니다!

Generative Model

• 생성모델은 단순히 “생성”만이 목적을 갖는 것은 아님
• 생성에 이어 분류/판별도 목적을 두고 있음
  • Generation : 확률분포 $p(x)$로부터 추출한 $x_{new}$가 특정 클래스를 띔
  • Density estimation : $p(x)$가 특정 클래스가 높게 나온다면 다른 것들은 낮게 나오게된다 (anomayly detection)
  • Unsupervised representation learning
• 그렇다면 여기서 $p(x)$는 어떻게 결정할까?
  • 2진 데이터는 Bernoulli dist’n $\rightarrow$ 1개의 parameter
  • 그외 여러개 데이터는 카테고리 분포를 사용함 $\rightarrow$ n-1개의 parameter

---

Auto-regressive Model

• AR 모델에 사용되는 중요한 3가지 규치
  • Chain Rule
    $p(x_1, …, x_n) = p(x_1)p(x_2|x_1)p(x_3|x_1,x_2)\cdots p(x_n|x_1,\cdots ,x_{n-1})$
  • Bayes’ Rule
  • Conditional independence
    $\text{If } x \perp y | z, \text{then } p(x|y,z) = p(x|z)$
• 28 X 28 binary 이미지를 생성한다고 하자
• $p(x) = p(x_1, …, x_{784})$를 예측해야함
  • chain rule에 따르면 $p(x_{1:784}) = p(x_1)p(x_2|x_1)p(x_3|x_{1:2})\cdots$
  • 이 처럼 이전 정보에 dependency 한 경우를 AR model이라고 함
  • binary pixel의 순서를 정하는 방법과 몇번재 이전 정보까지 depend할 지에 따라 성능이 달라짐

---

Variational Auto-encoder

• Auto Encoder는 Encoder에 들어온 입력에서 특징을 추출하여 입력의 압축정보를 latent variable에 담고 latent variable을 통해 다시 입력값을 복원함
• 수학적으로 보면 PCA와 유사한 의미를 지니고 있음
• 그렇다면 Latent Space로부터 데이터를 생성할 수는 없을까? 라는 관점에서 VAE가 주목을 받음

문제인식

• 문제는 기존에 갖고 있는 데이터들은 너무 고차원적이라 실제 데이터의 분포를 찾는 것은 불가능
  • 그렇다면 샘플들의 분포를 사전에 알고 있는 어떤 분포로 표현할 수 있을까?
  • 대표적으로 Latent Space가 가우시안 분포를 따른다면 평균과 표준편차만으로도 분포를 표현이 가능
    Posteriror distribution인 $p_{\theta}(z|x)$은 알기가 어려움
    $\rightarrow$ Variational distribution $q_\phi(z|x)$로 근사
• 따라서 실제 posterior와 variational distribution의 분포 차를 나타내는 KL-Divergence를 최소화하는 것이 목표

\[\begin{aligned} D_{KL}(p||q) & = \int p(x)\log\frac{p(x)}{q(x)}dx \\ & = \int p(x)\log p(x)dx - \int p(x) \log q(x) dx \end{aligned}\]

• KL-Divergence는 두 분포가 동일하면 0이 되고 계산순서가 바뀌면 값이 바뀔 수 있음
• Latent Space의 분포가 가우시안 분포를 따른다는 가정을 한 이유는 KL-Divergence가 가우시안 case에서 간략하게 표현이 가능하고 미분가능성을 갖기 때문

해결 접근

\[\begin{aligned} \ln{p_\theta (D)} & = \mathbb{E}_{q_\phi (z|x)}[\ln{p_\theta (x)}] \\ & = \mathbb{E}_{q_{\phi} (z|x)}\left[\ln\frac{\theta (x, z)}{p_\theta (z|x)} \right] \\ & = \mathbb{E}_{q_\phi (z|x)}\left[\ln\frac{p_\theta (x, z)q_\phi (z|x)}{q_\phi (z|x)p_\theta (z|x)} \right] \\ & = \mathbb{E}_{q_\phi(z|x)}\left[\ln\frac{p_{\theta} (x, z)}{p_\phi (z|x)} \right] + \mathbb{E}_{q_\phi (z|x)}\left[\ln\frac{q_\phi (x, z)}{p_\theta (z|x)} \right]\\ & = \underbrace{\mathbb{E}_{q_\phi (z|x)}\left[\ln\frac{p_\theta (x, z)}{q_\phi (z|x)} \right]}_{\text{ELBO}} + \underbrace{D_{KL}(q_\phi (z|x)||p_\theta (z|x))}_{\text{KL-Divergence}} \end{aligned}\]

• $D_{KL}(q_\phi(z|x)||p_\theta(z|x))$ 을 낮추는 것이 목적이지만 $p_\theta(z|x)$는 알아내는 것이 불가능하기 때문에 직접적인 objective를 줄이는 것은 불가능
• 전체 값은 상수로 일정하므로 ELBO를 키우면 간접적으로 KL-Divergence를 낮추는 것과 같은 효과를 줌

\[\begin{aligned} \mathbb{E}_{q_\phi(z|x)}\left[\ln\frac{p_\theta(x, z)}{q_\phi(z|x)} \right] & = \int\ln\frac{p_\theta(x|z)p(z)}{q_\phi(z|x)}q_\phi(z|x)dz \\\\ & = \mathbb{E}_{q_\phi(z|x)}[p_\theta(x|z)] - D_{KL}(q_\phi(z|x)||p(z)) \end{aligned}\]

• ELBO를 연산한 결과는 총 2개의 항이 존재하는데 앞부분을 Reconstruction Term이라고 함
  • encoder를 통해 데이터를 latent space에 보내고 그로부터 동일한 샘플이 나올 확률이 Likelihood
• 뒤쪽 KL-Divergence 부분은 prior fitting term이라고 함
  • 우리가 예측한 latent 분포와 prior 분포가 얼마나 차이가 있는지를 나타내는 값

Adversarial Auto-encoder

• VAE에서 prior fitting term을 GAN objective로 바꾼 것
• latent distribution을 smapling 가능한 distribution만 있으면 충분함

---

Genrative Adversarial Network (GAN)

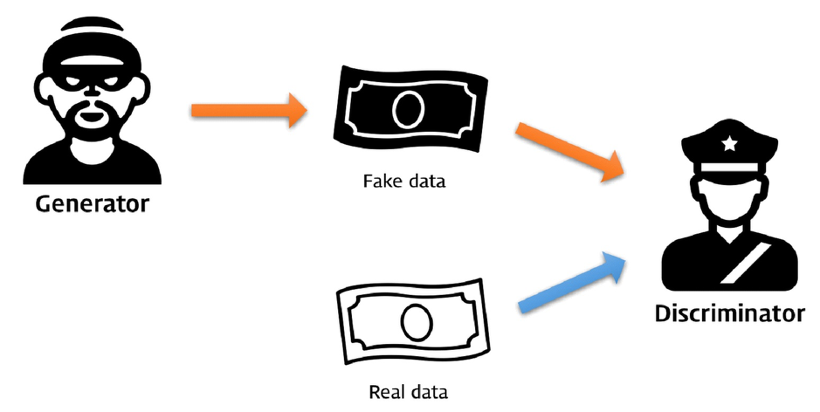
• GAN은 기본적으로 Two-ply minimax Game을 근간에 둔 모델
• 2개의 모델이 사용되며 Generator와 Descriminator가 서로 경쟁하며 학습을 진행
• 결과적으로 성능이 좋은 descriminator를 얻어냄

\[\begin{aligned} \begin{matrix} \text{Discriminator : } \quad \underset{D}{\max}V(G,D) = E_{\mathbf{x} \sim p_{\text{data}}}[\log D(\mathbf{x})] + E_{\mathbf{x} \sim p_{G}}[log(1 - D(\mathbf{x}))] \\ D^{*}_{G}(\mathbf{x}) = \frac{p_{data}(\mathbf{x})}{p_{data}(\mathbf{x})} + p_G(\mathbf{x}) \end{matrix} \end{aligned}\]

• 기본적인 컨셉이 Two-ply minimax Game이라 generator와 descriminator는 각자의 선택 중 항상 최선을 선택함 (minimax game이란?)
• generator가 fix된 상황에서 항상 최적으로 결과를 분류하는 discriminator를 $D^{*}_{G}$라고 함

\[\begin{aligned} \text{Generator : } \quad \underset{G}{\min}V(G,D) = E_{\mathbf{x} \sim p_{\text{data}}}[\log D(\mathbf{x})] + E_{\mathbf{x} \sim p_{G}}[log(1 - D(\mathbf{x}))] \end{aligned}\]

• 이렇게 나온 학습을 통한 $D$를 기반으로 generator가 학습을 함