[BoostCamp AI Tech / Level 1 - DL Basic] Day14 - Convolutional Neural Networks

DL Basic : Convolutional Neural Networks

---

Convolution

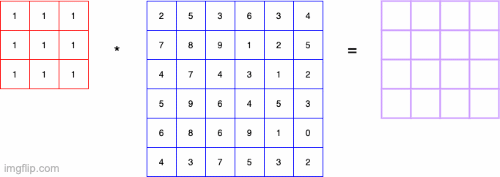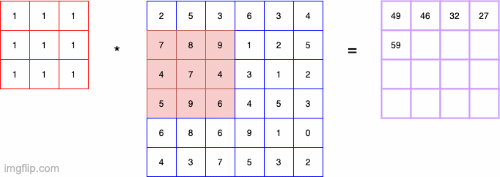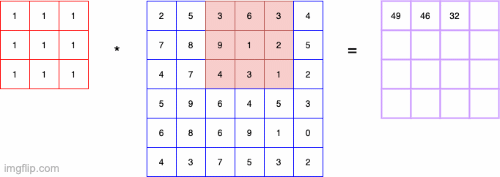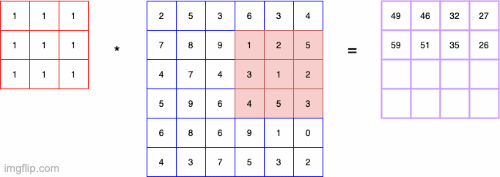
• convolution 연산은 기본적으로 Input에 대해 커널단위로 연산을 하는 것을 의미
• 특징 추출을 목적으로 할 때 많이 사용함
• 필터(kernel)의 종류에 따라 다른 결과가 나타남
  • ex) convolution filter가 3X3이고 value가 모두 1/9이면 이미지의 평균이 convolution의 output이 되어 Blur효과와 같은 결과가 나타남
    $\rightarrow$ 전반적으로 기존 이미지보다 수치가 평균적으로 낮아진 것
• 자세한 내용은 수학적 의미의 CNN 참고

RGB Convolution

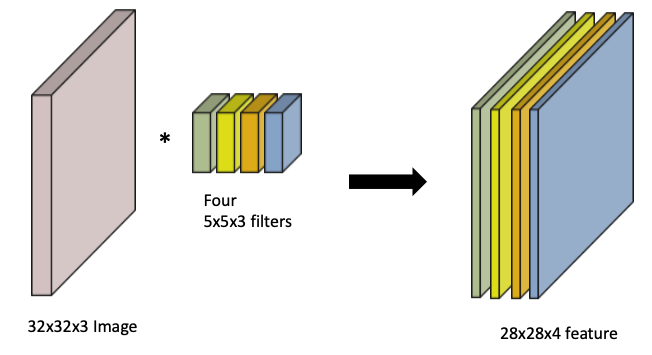
• 기본적인 convolution 연산의 원리에 따라 사용된 필터의 개수는 최종 결과의 feature scale을 결정
• 위의 사진처럼 4개의 filter를 사용하면 4개의 특징이 추출된 결과가 나타남

Stack of Convolutions

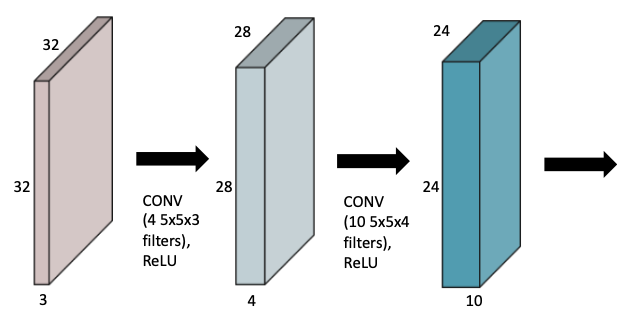
• CNN의 핵심은 파라미터 수를 줄이는 것에 있기 때문에 convoluton 연산에 사용된 전체 파라미터를 계산하는 것이 중요

\[\text{\# of Paramter} = \text{Kernel size} \times \text{\# of Input Channel} \times \text{\# of Output Channel}\]

---

Convolution Neural Networks (CNN)

• CNN은 크게 2가지 구조로 구성됨
  • Convolution ans pooling layers : feature 추출
  • Fully connected layer : decision making
• 최근에는 Fully connected를 없애는 추세
  • Fully Connected는 dimesion에 맞춰 weight를 가지므로 parameter 수가 급격하게 증가하는 영향을 줌
  • parameter 수가 증가하면 학습 난이도가 높아지고 generalization performance가 낮아짐

Stride

• stride란 kernel이 움직이는 반경을 말함
• 위의 사진에 따르면 stride는 1임
• stride에 따라 output의 크기가 달라짐

Padding

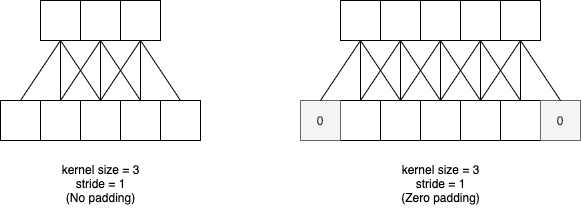
• Padding은 boundary에 버려지는 convolution 연산을 처리해주는 역할을 함
• 사진처럼 zero padding이 주어지면 input dim과 output dim을 동일하게 할 수도 있음

Convolution Parameters

• CNN의 parameter를 계산할 때 padding, stride는 고려하지 않아도 됨
• Kernel size, input channel size, output channel size를 모두 곱해주면 됨

1 X 1 Convolution

• 약간 특수한 convolution 연산
• 실제로 이미지에서 뭔가 특징을 추출하거나 하는 역할을 하지는 않음
• convolution 연산의 특성상 channel size를 바꿔주는 역할을 함
• 보통 큰 input channel을 reduction하는 과정에 사용

---

Modern CNN

• CNN은 시대별로 변화하는 핵심 특징은 크게 3가지가 있음
  • network depth 증가
  • number of parameter 감소
  • performance 향상

AlexNet

• AlexNet은 CNN의 초석을 다진 모델
• Key ideas
  • ReLU
  • GPU implementation
  • pooling
  • data augmentation
  • Dropout
• 지금보면 매우 당연한 것들이지만 원래 당연한걸 시작한 것들이 대단한 법인 것처럼 AlexNet은 지금의 CNN 모델의 시작이었음
• 기존의 sigmoid나 tanh와 같은 activation function의 gradient 소멸 문제를 해결하고자 ReLU를 사용함
• 한계점은 kernel에서 11 X 11을 사용했다는 점으로 영역은 넓지만 parameter를 늘리게 된다는 것

VGGNet

• VGGNet은 3 X 3 convolution filter만 사용
• Dropout은 0.5로 설정했음
• layer의 수에 따라 VGG16, VGG19로 구분

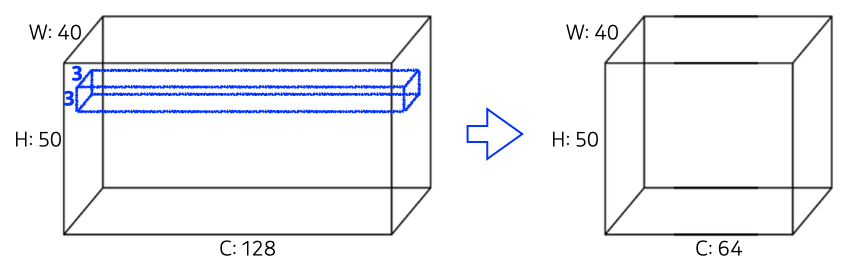
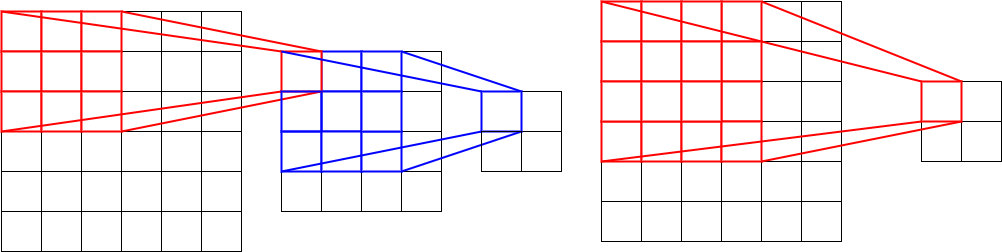channel size가 모두 128이라하자

• 3 X 3만 사용한 것은 같은 연산이라도 parameter를 더욱 줄이기 위한 방법
• 두 convolution 연산결과는 동일
• 하지만 parameter는 차이가 큼
  • 3 X 3 : $3 \times 3 \times 128 + 3 \times 3 \times 128 = 294912$
  • 5 X 5 : $5 \times 5 \times 128 \times 128 = 409600$
• 이는 제곱연산의 수치 증가 폭이 숫자에 비례해서 커지기 때문에 나타나는 현상

GoogLeNet

• GoogLeNet은 비슷한 네트워크가 반복되는 Networ in Network(NiN)방식을 사용
• 핵심은 NiN은 활용한 inception blocks

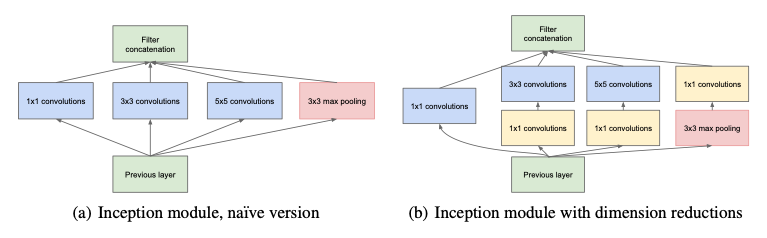
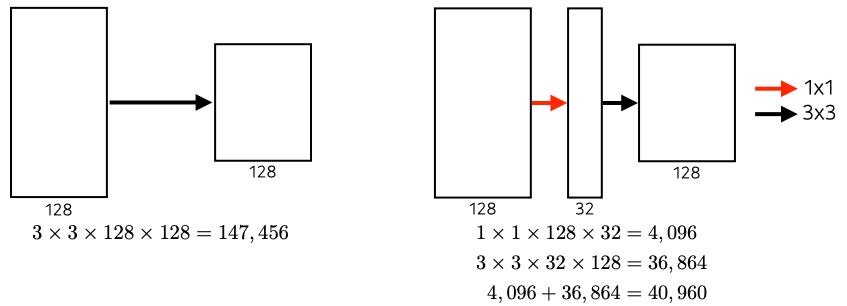
• inception block은 여러 response를 합치는 것도 있지만 핵심 역할은 parametr 수의 감소
• 앞서 1 X 1 convolution에서 설명한 아이디어를 활용
• 각 연산 앞이나 뒤에 1 X 1 Conv를 적용하여 channel의 dimension을 줄이는 방법을 활용함

ResNet

• ResNet은 딥러닝의 Deep의 가치를 높여준 모델

• Deep learning이란 이름에 맞다면 층이 깊어질수록 성능이 좋아야하는데, 실제로는 그렇지 않다는 것이 항상 문제였음
• 일정 layer 개수를 초과하면 오히려 성능이 떨어지는 결과가 나타남
• ResNet은 identity map을 통해 이를 해결함

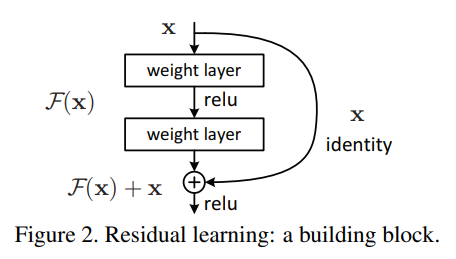
• 사실 layer의 수가 많아지면 성능이 떨어지는 이유는 Vanishung Gradient때문이었으므로 이를 해결하는 것이 목적
• 이전 층까지 학습된 결과와 추가된 레이어의 출력의 차이인 Residual만 학습하면 된다는 아이디어를 적용

DenseNet

• ResNet의 아이디어를 확장한 개념
• ResNet은 이전 층까지의 결과를 합치기 때문에 결과에 직접적인 영향을 주는 것이 문제가 될 수 있음
• 따라서 이전 측 결과를 합하는 게 아닌 concatenation, 즉 행렬적으로 값을 붙이는 방식을 활용
• 이때 channel 크기가 기하급수적으로 커지는 것을 막고자 채널 증폭 후 1X1 Conv를 활용한 dimension 감소를 반복하는 방식을 사용