DL Basic : Optimization

Introduction

Model 학습의 기본적인 원리는 Gradient Descent
Gradient Descent는 1차 미분의 결과의 최적화 알고리즘
- 1차 미분 결과의 최적화는 local minimum을 찾는 것

Important Concepts in Optimization

Generalization

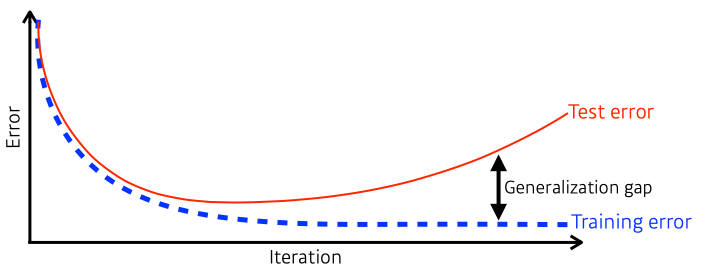
Generalization은 모델의 성능으로 사용함
좋은 generalization performance는 Network의 성능이 train과 비슷한 것을 의미
- 하지만 기본적인 train set 성능이 낮으면 generalization performance가 좋아도 모델 성능 자체가 좋지 않을 수 있음
Overfitting(과적합) 과 Underfitting을 방지하는 것이 generalization의 가장 핵심적인 포인트

Cross-validation

K-Fold validation이라고도 함
학습 data가 적은 경우의 문제를 해결하고자 등장
전체 train data를 n등분하여 k번째 등분을 validaation data로 설정하고 n-k개의 데이터를 train으로 설정하여 학습을 하는 과정
n개의 valid set으로 검증하는 과정과 같음
일반적으로 cross-validation을 통해 최적 hyper parameter를 탐색하고 최종적으로 전체 데이터로 모델을 학습함

Bias / Variance

Variance : 유사 input에 대해 prediction이 얼마나 비슷한가?
Bias : 전반적인 prediction이 target과 얼마나 떨어져있는가?

\[\begin{aligned} \mathbb{E}\left[ (t-\hat{f})^2 \right] & = \mathbb{E}\left[ (t-f + f-\hat{f})^2 \right] \\ & = \mathbb{E}\left[ (f - \mathbb{E}[\hat{f}]^2)^2 \right] + \mathbb{E}\left[ (\mathbb{E}[\hat{f}] - \hat{f})^2 \right] + \mathbb{E}[ \epsilon ] \end{aligned}\]

위 공식은 cost 에 대한 bias와 variance, noise의 관계성을 나타낸 것
공식에 따라 bias, variance, noise는 tradeoff 관계를 가짐

Booststraping

데이터 셋에서 subsampling을 통해 여러 데이터 셋을 형성하고 그에 맞는 여러 모델들을 만드는 기법
형성된 model들의 예측값들을 보고 예측의 consensus(일관성)로 전반적인 uncertainty를 판단
보통 앙상블(Ensemble)기법에 많이 활용됨

Bagging VS Boosting

Bagging (Bootstrapping aggregating)
- 여러 모델들의 학습결과를 합쳐서 판단하는 방법
- 가장 좋은 결과를 선택하는 voting이나 평균치를 연산하는 averaging을 활용해서 정답을 도출
Boosting
- 모델을 여러개 만드는 것은 동일하지만 연속적으로 연결시켜 이전에 좋지 않은 결과를 보이는 case를 집중적으로 학습함
- 여러개의 weak learner를 합쳐서 1개의 strong model을 형성

Gradient Descent Methods

Stochastic Gradient Descent : 1번에 1개의 데이터를 활용해서 gradient를 update
Mini-batch gradient Descent : batch-szie sample을 활용해서 gradient를 update
Batch Gradient Descent : 전체 데이터를 활용해서 gradient를 update
보통 min-batch 방식이 효과가 좋은 것으로 알려져있음

Batch-Size

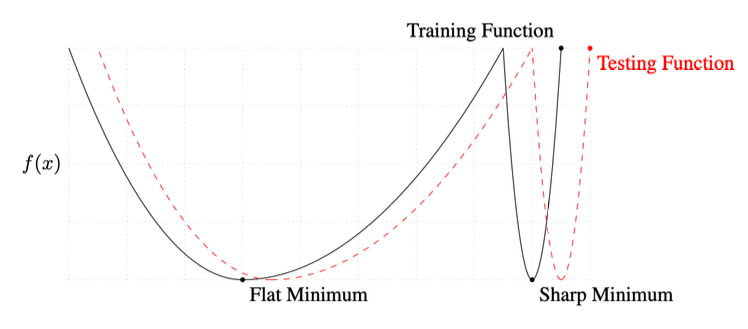
batch-size를 적절히 잘 조절하는게 학습과정의 핵심
이때 보통 작은 batch-size가 더 효과가 좋은데, 이는 small-batch method는 flat minimizer이기 때문임
- 그림을 보면, flat minimum에서는 prediction이 target에서 벗어나도 실제 값이 큰 차이를 보이지 않음
- 하지만 sharp minumum은 prediction이 약간만 벗어나도 매우 큰 오차를 갖게되는 것을 볼 수 있음

Gradient Descent & Momentum

\[\begin{aligned} W_{t+1} \leftarrow W_{t} - \eta g_{t} \end{aligned}\]

$\eta$ : learning rate
$g_{t}$ : gradient
일반적으로 알고있는 gradient descent

\[\begin{aligned} & a_{t+1} \leftarrow \beta a_{t} + g_{t} \\ & W_{t+1} \leftarrow W_{t} - \eta a_{t+1} \end{aligned}\]

$a_{t+1}$ : accumulation
$\beta$ : momentum
momentum의 역할은 진행한 gradient의 방향을 유지해주는 역할
수식을 보면 이전의 학습결과에 momentum을 처리해서 반영
학습을 하다보면 batch에 따라 oscillation의 형태로 gradient가 움직이는 경우가 있는데, 이때 momentum이 적용되면 이를 어느정도 보완해줄 수 있음

Nestrov Accelerated Gradient (NAG)

\[\begin{aligned} & a_{t+1} \leftarrow \beta a_{t} + \nabla\mathcal{L}(W_{t} - \eta\beta a_{t}) \\ & W_{t+1} \leftarrow W_{t} - \eta a_{t+1} \end{aligned}\]

$\nabla\mathcal{L}(W_{t} - \eta\beta a_{t})$ : Lookahead gradient
NAG는 momentum의 최적값을 지나치는 문제를 방지하는 목적을 갖고 있음
- lookahead gradient는 momentum에의해 이동하는 곳에서 gradient를 계산하여 적용한 것

Adagrad

\[\begin{aligned} W_{t+1} = W_t - \frac{\eta}{\sqrt{G_{t} + \epsilon}} g_{t} \end{aligned}\]

$G_{t}$ : Sum of gradient squares
$\epsilon$ : for numerical stability
Adagrad의 핵심 아이디어는 learning rate를 건드린다는 것
- $G_{t}$에 이전 gradient들의 제곱이 누적되기 때문에 많이 변화한 parameter의 학습률을 낮추고 적게 변화한 parameter의 학습률을 높이는 방식을 선택
$\epsilon$은 0으로 나누는 것을 방지하는 상수
Adagrad는 $G_{t}$가 너무 커지면 더 이상 학습이 일어나지 않는 문제가 발생

Adadelta

\[\begin{aligned} G_t = \gamma G_{t-1} + (1-\gamma)g_{t}^2 \\ W_{t+1} = W_{t} - \frac{\sqrt{H_{t-1} + \epsilon}}{\sqrt{G_{t}+\epsilon}}g_t \\ H_t = \gamma H_{t-1} + (1-\gamma)(\Delta W_t)^2 \end{aligned}\]

$G_t$ : EMA of gradient squares
$H_t$ : EMA of differentce squares
Adadelta에서 $G_t$와 $H_t$는 $\gamma$가 recursive한 값으로 영향을 주므로 time의 영향을 받게 적용함 (Exponential Moving Average)

RMSprop

\[\begin{aligned} G_t = \gamma G_{t-1} + (1-\gamma)g_{t}^2 \\ W_{t+1} = W_{t} - \frac{\eta}{\sqrt{G_{t}+\epsilon}}g_t \end{aligned}\]

RMSprop은 공식적으로 출판한 내용은 없고 그냥 이런식으로 하니 잘 되었다~ 라는 식으로 등장
이전에 Adagrad는 stepsize가 없었는데, 이를 수정하여 stepsize를 적용함

Adam

$m_t = \beta_1 m_{t=1} + (1-\beta_1)g_t \\ v_t = \beta_@ v_{t-1} + (1-\beta_2)g_t^2 \\ W_{t+1} = W_t - \frac{\eta}{\sqrt{v_t + \epsilon}}\frac{\sqrt{1-\beta_2^t}}{1-\beta_1^t}m_t$

$m_t$ : momentum
$v_t$ : EMA of gradient squares
$\frac{\sqrt{1-\beta_2^t}}{1-\beta_1^t}$ : unbiased estimator
Adam은 momentum에 RMSprop 개념이 합쳐진 방식
단, 연산에서 지수평균을 사용

Regularization

Early Stopping

test set을 활용해 학습을 하는 것은 cheating이므로 valid set의 결과를 활용해 특정 metric 조건에 맞춰 학습을 조기멈춤하는 것

Parameter Norm Penalty

\[\text{total cost} = \text{loss}(\mathcal{D}; W) + \frac{\alpha}{2}\lVert W \rVert_2^2\]

weight decay라고도 함
parameter 폭발을 방지하는 것이 목적임

Data Augmentation

주어진 데이터의 방향 혹은 거울상과 같은 다양한 변형을 취하는 것을 의미
더 많은 데이터셋을 위해 자주 사용
이미지 분류 문제에서 많이 사용

Noise Robustness

input이나 weight에 노이즈를 추가하는 것

Label smoothing

Mix-up, CutMix같은 방식을 통새 label의 decision boundary 처리를 도와주는 것
이미지 처리를 할 때 두 개의 label을 섞은 이미지를 사용하는 Mixup이나 일부를 잘라서 하비는 cutmix 데이터를 활용하면 더 좋은 학습 성능을 보이기도 함

Dropout

forward 과정에서 일정 확률로 랜덤하게 neuron의 연결 가중치를 0으로 설정하는 것
1개의 모델 구조에서 뉴런 구성을 변경하기 때문에 마치 여러개의 모델을 학습하는 것과 같은 효과를 가짐

Batch Normalization

\[\begin{aligned} & \mu_{B} = \frac{1}{m}\sum_{i=1}^m x_i \\ & \sigma^2_{B} = \frac{1}{m}\sum_{i=1}^m (x_i - \mu_{B})^2 \\ & \hat{x}_i = \frac{x_i - \mu_{B}}{\sqrt{\sigma^2_{B}+\epsilon}} \end{aligned}\]

Batch 정규화는 Gradient Vanishing/Exploding 문제를 해결하고자 등장
각 배치별로 데이터를 정규화하여 0 ~ 1의 수치로 조정

[BoostCamp AI Tech / Level 1 - DL Basic] Day13 - Optimization