[BoostCamp AI Tech / Level 1 - DL Basic] Day13 - MLP (Multi-Layer Perceptron)

DL Basic : MLP (Multi-Layer Perceptron)

---

Neural Networks

• 일반적으로 Neural Netwrok라고 하면 인간의 뇌 구조를 모방해서 만든 시스템이라고 생각함
• 하지만 우리의 비행기가 새를 모방했다고 하지만 새와는 다른 것처럼 Neural Net이 정확하게 인간의 뇌를 구현한 것이라 보긴 어려움
• Neural Net의 실질적 정의는 function approximators가 적합
  • Affine transformations : layer간의 연산은 행렬 연산인 affine 연산을 사용
  • Nonlinear transforamtions : layer 중간에 activation function을 추가하여 non-linear 변환을 진행

Linear Neural Networks

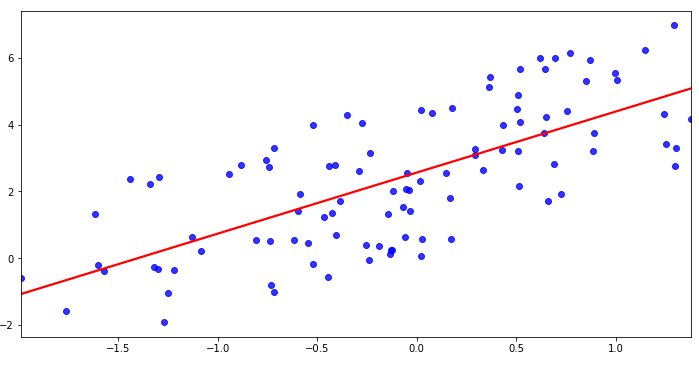
• Linear NN은 기본적으로 정답모델을 찾을 때 각 parameter에 따라 편미분을 활용한 backpropagation을 진행

\[\begin{aligned} w \leftarrow w - \eta \frac{\partial \text{loss}}{\partial w} \\ b \leftarrow b - \eta \frac{\partial \text{loss}}{\partial b} \end{aligned} \quad\quad \eta : \text{stepsize}\]

• loss값을 backpropagation을 통해 update할때
• stepsize값을 잘 고려하는 것이 중요

---

Multiplayer Perceptron

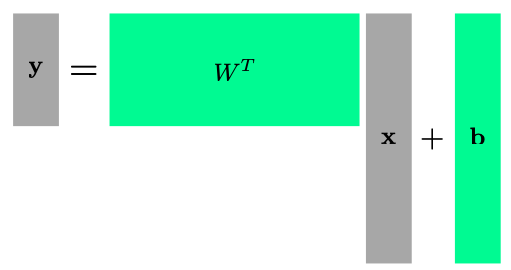
• Affine transform은 linear NN의 핵심 중 하나
• weight matrix의 역할은 x의 input dimension을 y dimension으로 vector space를 변환해주는 역할을 함
  • 선형대수학에선 변환을 행렬로 표현

\[y = W_3^{\intercal} \mathbf{h}_{2} = W_{3}^{\intercal}\rho(W_{2}^\intercal\mathbf{h}_{1}) = W_{3}^{\intercal}\rho(W_{2}^\intercal\rho(W_{1}^\intercal\mathbf{x}))\]

• hidden layer ($\mathbf{h}_{n}$)을 통과한 값에 activation function($\rho$)을 적용하지 않으면 단순히 weight matrix간의 행렬 곱이 되므로 큰 의미가 없음
• 따라서 hidden layer value에 non-linear function인 activation function을 추가해줌
• Multilayer feedforward networks are universal approximators에 따르면 hidden layer가 1개라도 있으면 대부분의 continuous function을 포함하기 때문에 우리가 찾고자하는 모델 구조가 존재함을 보장

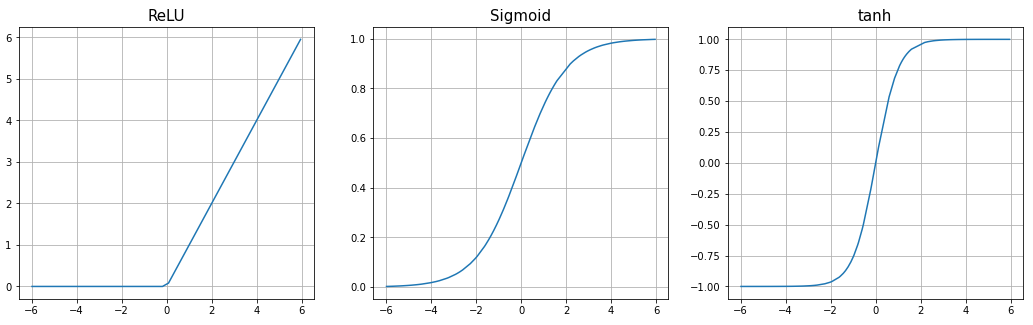Activation function 종류

Loss function

\[\begin{aligned} \text{Regression Task} & \qquad & \text{MSE} = \frac{1}{N} \sum_{i=1}^{N} \sum_{d=1}^{D}(y_{i}^{(d)} - \hat{y}_{i}^{(d)})^2 \end{aligned}\]

• MSE를 많이 사용하지만 모델의 목적에 따라 알맞은 loss function을 선택해야함
• MSE의 경우 반드시 squared로 계산할 필요는 없음
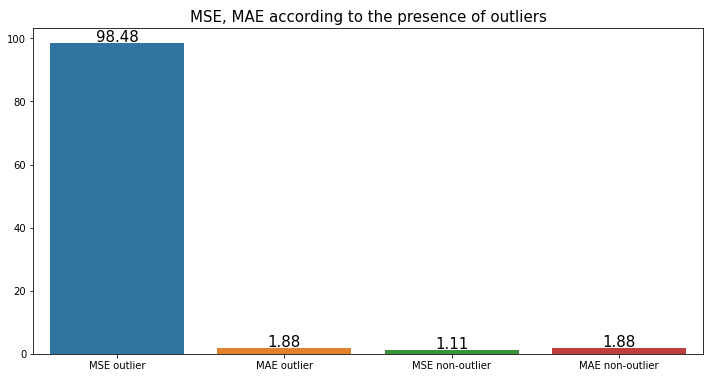
  • MSE는 오차의 제곱을 연산하므로 outlier target 발생시 loss 값이 급격하게 커져 전체 neural net을 망가트릴 수도 있음
  • 이 경우 오차의 절댓값의 합을 연산하는($L_1$) MAE가 적당한 경우도 있음

\[\begin{aligned} \text{Classification Task} & \qquad & \text{CE} = -\frac{1}{N} \sum_{i=1}^{N} \sum_{d=1}^{D}y_{i}^{(d)} \log\hat{y}_{i}^{(d)} \end{aligned}\]

• Cross Entropy는 보통 분류문제에서 많이 사용되는 Loss
  • 예측의 probability가 정답 클래스가 아닌 경우에 값이 클수록 $\log$ 연산에 의해 값이 증폭되는 현상이 나타남

\[\begin{aligned} \text{Probablistic Task} & \qquad & \text{MLE} = \frac{1}{N} \sum_{i=1}^{N} \sum_{d=1}^{D}\log \mathcal{N}(y_{i}^{(d)};\hat{y}_{i}^{(d)}, 1) & \qquad \text{(=MSE)} \end{aligned}\]

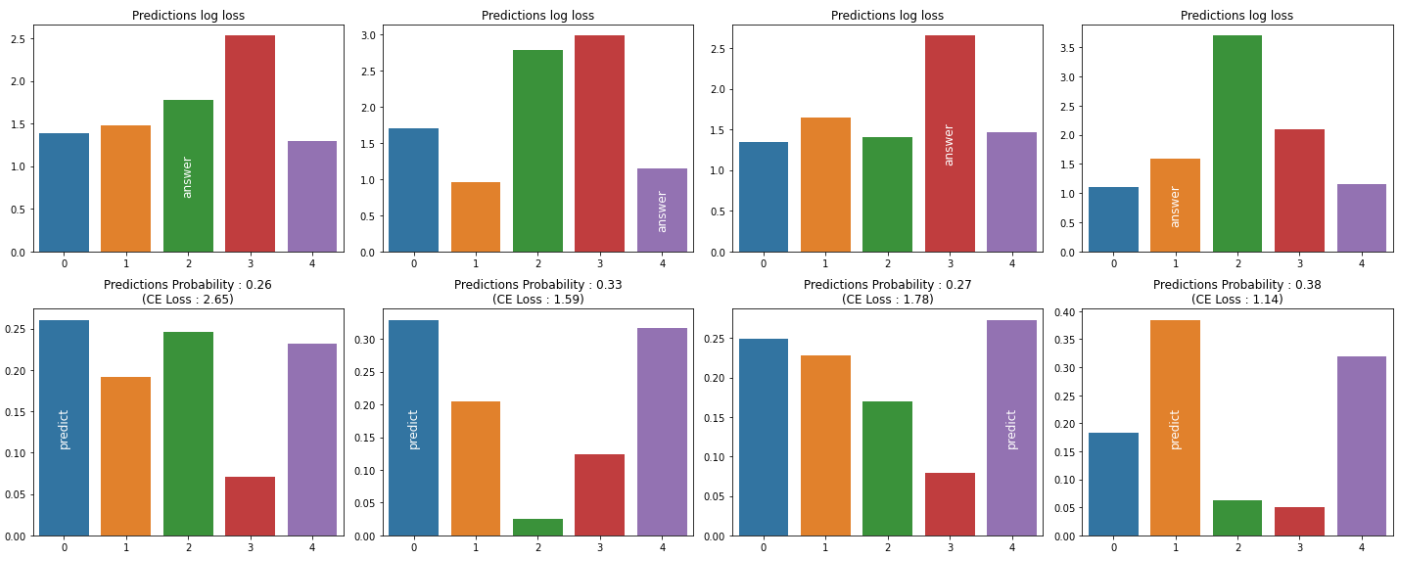
• MLE는 확률적 연산이 사용되는 loss function