[Data Structure] Vector and List (벡터와 리스트)

Vector (벡터)

벡터 개념

벡터는 크기가 동적으로 변하는 배열이라고 생각하면 된다. Array list라고 부르기도 하며 다양한 데이터들이 배열의 형태로 저장된 연속체라고 생각하면 된다.
삽입, 삭제, 접근 연산이 모두 index에의해 이뤄지게 된다.

Vector ADT

벡터의 추상자료형은 다음과 같다.

• at(integer i) : index i에대해서 데이터 값을 반환해준다.
• set(integer i, object o) : index i의 데이터를 o로 바꿔준다.
• insert(integer i, object o) : index i에 o를 삽입한다.
• earase(integer i) : index i에 있는 데이터를 제거해준다.
• size() : 벡터의 크기를 반환해준다.
• empty() : 벡터가 비었는 지를 알려준다.

벡터의 시간복잡도

• 벡터는 위에서 말했듯이 링크드 리스트와 다르게 인덱스로 모든 데이터에 접근하여 삽입, 삭제가 이뤄진다. 그렇기 때문에 해당 인덱스의 데이터를 가져오거나, 설정해주는 at과 set은 $ O(1)$ 의 시간복잡도를 갖는다.
• 그러나 삽입연산과 삭제연산을 하는 inset와 remove는 $ O(n)$ 의 시간복잡도를 갖는데, 이유는 해당 인덱스의 값을 넣거나 삭제를 함과 동시에 그 이후의 데이터들을 모두 움직여줘야 하기 때문이다. 하지만 이것은 선형 배열로 구현할 경우이고, 원형 배열기반으로 구현하면 이 또한 $ O(1)$ 의 시간복잡도로 구현할 수 있다.
  자세한 설명은 구현에서 설명하겠다.

Array-based Vector

벡터를 구현할 때 보통 배열 기반으로 구현하게 된다. 기존 C++STL에 있는 벡터는 초기에 설정된 크기를 넘는 경우에는 이전에 있는 크기의 2배만큼으로 크기를 늘려주게된다. 이러한 방법을 사용해도 괜찮고, 원형 배열을 사용하는 경우도 있다. 원형 배열을 사용하는 방식은 간단히 설명하고 넘어가겠다.

Vector by Circular Array

원형 배열 기반의 벡터에 대해서 자세한 설명은 삽입연산과 삭제연산의 원리에 대해서만 설명하겠다. 그 외는 단순히 값을 반환하거나 바꿔주기만 하면 되는 간단한 대입연산이다.

삽입연산

배열 기반 벡터는 가장 앞의 인덱스를 알려주는 f와 가장 뒤의 인덱스+1을 알려주는 r이 있다. 일반적으로 데이터가 들어가 있을 때, f는 가장 앞의 데이터가 저장된 인덱스를 가리키고 있다.
즉 사용자 입장에서는 0번 인덱스에 f가 있다. 하지만 실제로 사용되는 배열은 원형 배열이라 f의 인덱스가 반드시 0번이라는 보장은 없다.
그래서 보통 삽입 연산의 방식은 A[(f + i) % n] = o의 형식으로 작성된다.
문제는 가장 앞에 데이터를 삽입하는 경우인데, 이 경우에는 f-1로 이동시켜서 값을 넣어주면된다.
하지만 0번 인덱스에서 -1을 하는 문제를 막기위해서 A[(f-1+n)%n]의 방식으로 작동시켜준다. 삭제연산도 유사한 원리로 작동한다.

Vector by Normal Array

일반적인 배열로 벡터를 구현을 할 경우는 앞서 말한 원리처럼 배열의 크기를 늘려주는 작업도 고려해야한다.
배열의 크기를 늘리는 전략에는 2가지 전략이 있는데, Incremental strategy와 Doubling strategy가 있다.
Incremental Strategy는 상수 크기만큼 배열의 크기를 증가시키는 것이다. 100->200->300…처럼 특정 상수 크기만큼 증가시킨다.
Doubling Strategy는 이전 크기의 2배만큼 크기를 증가시킨다. 100->200->400 이런 식으로 증가시키며 일반적인 벡터의 크기 증가 방법이 이렇다.

삽입연산

일반 배열로 구현한 벡터의 삽입연산은 아래와 같이 작성할 수 있다.

Algorithm inset(o)
  if n = N then
    N <- 2N {Doubling}
    A <- new array of size N

    for i<-0 to n-1 do
      A[i] <- S[i]

    delete S

    S <- A

  S[n] <- o
  n <- n+1

우선 크기를 늘릴 배열 A를 새롭게 선언해준다. 당연히 선언 이전에 N의 크기는 2배로 늘려준다. 그 후 기존 배열을 삭제하기위해 기존 배열의 데이터를 새로 만든 A에 복사해준다. 그 후 S를 A로 대입해주면 된다. 이렇게 하면 Doubling Strategy를 활용한 기존의 벡터를 구현할 수 있다.

List

리스트는 앞선에서 배운 링크드 리스트관련의 C++ STL이다. 이미 C++ 기본 라이브러리에 구현이 되어 있으며 리스트는 인덱스가 아닌 position이라는 개념을 활용한다.

Position ADT

리스트는 벡터나 배열형태의 자료구조에서 사용되는 index를 사용하지 않고 memory상의 주소를 갖고있는 position이라는 개념을 사용한다. 해당 데이터가 저장되어있는 위치를 가져온다.
대표적인 예시로는…

• 배열의 cell도 position이다 물론 배열은 position이 아니라 index라고 부른다.
• 링크드 리스트의 노드

주소를 저장하고 있다는 점에서 문득 스쳐지나가는 개념이 하나 있다면 C++에대한 기초공부를 굉장히 잘했다고 볼 수 있다. C++에는 따로 멤버함수로 position을 가지고 있지 않고 주소값을 가지고 있는 포인터(pointer)를 갖고있다.

Node List ADT

리스트의 추상 자료형은 다음과 같은 것들이 있다.

• size(), empty() : 앞선에서도 많이 다룬 것들이다.
• iterator
  • begin() : 리스트의 시작부분의 주소를 반환해준다.
  • end() : 리스트의 마지막부분의 주소를 반환해준다.
• insertFront(e), insertBack(e)
• removeFront(), removeBack()
• insert(position, e)
• remove(position)

이전에 다뤘던 ADT들과 조금 다른 것이 추가되었다.
바로 iterator라는 개념이다. 실제로 벡터나 리스트관련을 STL로 사용할 때 자주 사용하게되는 개념이다.
iterator는 일종의 navigater역할이다. position이 확장된 개념인데 주소 값을 지시하는 역할을 하게된다. 여기서 end()를 마지막 주소를 반환해준다고 했는데, 실제로는 마지막의 다음 주소를 가지고 있다. 그래서 보통 반복문으로 iterator를 변경할 때, 조건문에는 i.end()와 같지 않을 때까지라는 조건을 붙인다.
가장 마지막의 2개 함수는 특정 iterator 위치에 값을 삽입하거나 삭제해주는 함수이다.

Doubly Linked List (이중 연결 리스트)

1일차에 우리는 Singly Linked List를 배웠다. 티스토리 블로그에는 간단하게 언급한 것 같은데, 여기서 언급했는 지는 기억이 잘 안난다.
링크드 리스트에는 종류가 보통 3가지가 있는데, 우리가 처음에 배운 단순 연결리스트, 이중 연결리스트, 환형(원형) 연결리스트가 있다.
이번에 다룰 내용은 실제 C++ STL로 사용되는 이중 연결리스트를 다뤄보겠다.

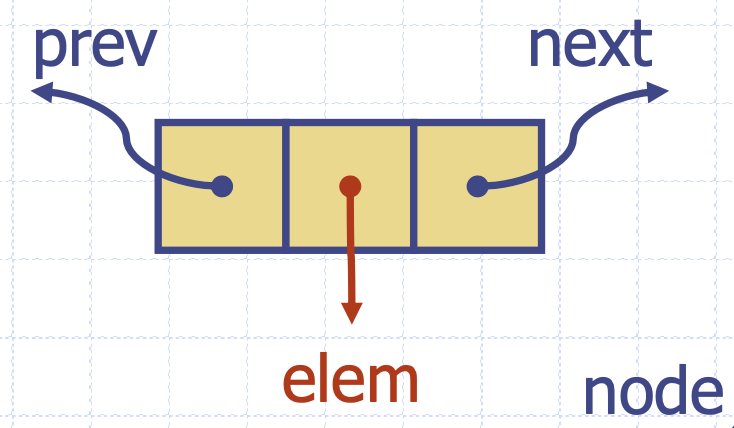
이중 링크드 리스트에 사용되는 노드는 단일 링크드 리스트의 노드에 1개의 주소필드가 추가된다.
기존의 노드는 next라는 다음 노드를 지시하는 주소필드가 존재했지만 새로 만드는 노드는 prev라는 이전 노드를 지시하는 주소필드가 존재한다. 그렇기 때문에 단순 연결리스트의 한계인 중간에 데이터 삽입하기가 가능해진다.

이중 연결리스트는 삽입과 삭제 함수의 일관성을 위해서 header와 trailer라는 dummy node가 존재한다. header의 prev와 trailer의 next는 모두 NULL값을 가리키고 있다.
이중 연결리스트를 구현해보면서 자세한 원리를 설명하겠다.

Doubly Linked list implementation (이중 연결리스트 구현)

Node class and prototype

#include <iostream>
using namespace std;

class Node {
public:
  int data;
  Node* next;
  Node* prev;

  Node() {
    next = prev = NULL;
    data = 0;
  }
  Node(int e) {
    this->data = e;
    this->next = NULL;
    this->prev = NULL;
  }
  ~Node() {}
};

class DLinkedList {
public:
  Node* head;
  Node* tail;
  int size;

  DLinkedList();
  void insertFront(int e);
  void removeFront();
  void insertBack(int e);
  void removeBack();
  bool empty();

  void insert(iterator iter, int e);
  void remove(iterator iter);

  ~DLinkedList(){}
}

맨 앞이나 맨 뒤에서의 삽입, 삭제 연산은 간단하지만 중간에 삽입하는 함수를 구현하기 위해서는 iterator class를 구현해서 만들어줘야한다. 하지만 iterator를 구현하는게 이 글의 목적이 아니므로 iterator는 생략한다.

initializer (생성자)

DLinkedList() {
  this->size = 0;
  this->head = new Node();
  this->tail = new Node();
  head->next = tail;
  tail->prev = head;
}

이중 링크드 리스트의 생성자에서는 앞서 말한 더미 노드가 구현이 된다. 그래서 head와 tail에 각각 새로운 노드를 만들어준다. 여기서 왜 head = tail = new Node();냐고 생각이 든다면 한 10초정도 잘 생각해봐라. 그래도 모르겠다면 음… 지금 이걸 공부할 때가 아닌 것 같다.

empty function

bool empty() {
  return head->next == tail;
}

예외처리를 위해 항상 먼저 만드는 empty함수이다. 원리는 항상 간단하다. head의 다음이 tail이면 빈 경우라고 생각하면된다.

insertFront function

void insertFront(int e) {
  Node* v = new Node(e);

  v->next = head->next;
  v->prev = head;
  head->next->prev = v;
  head->next = v;
}

노드를 2개나 변경시켜야하므로 상당히 헷갈리는 과정이 있다. 노드를 연결할 때 순서가 꼬이면 자기자신으로 도는 경우가 발생할 수 있으므로 순서를 잘 생각해야한다.
이전에 있던 노드를 먼저 변경하면 문제가 발생할 수 있으므로 새 노드를 우선 연결해주는게 좋다.

1. 삽입을 위한 노드를 새로 만들어준다.
2. 새 노드의 next를 head의 next 노드로 연결해준다.
3. 새 노드의 prev를 head로 해준다.
4. head노드의 다음 노드의 prev는 v를 가리킨다.
5. head노드의 next는 v를 가리킨다.

위의 순서에서 가장 헷갈리는 게 4번과 5번과정인데, 4번이 앞서야 하는 이유는 간단하다. 만약 head 노드의 next를 먼저 바꿔버리면 기존에 head의 다음 노드가 가리키는 이전 노드를 변경할 수 없게된다. 글로는 헷갈리니 아래의 사진을 참고해주길 바란다.

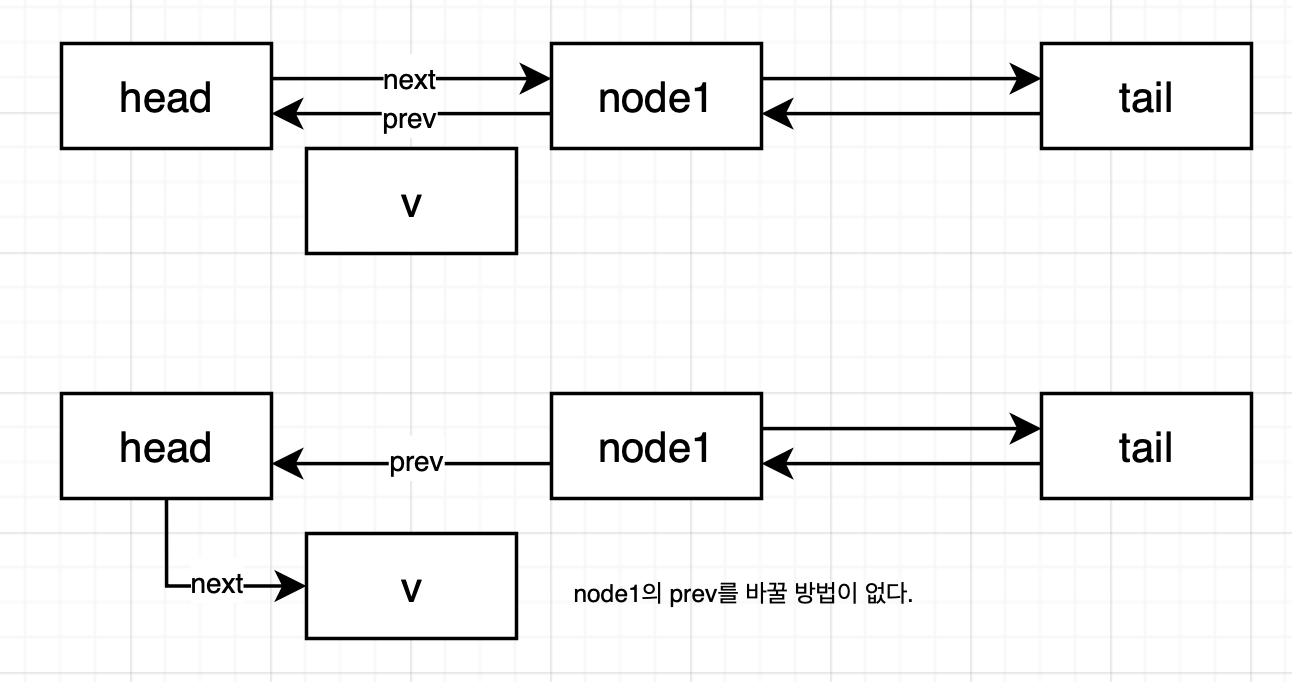
removeFront function

void removeFront() {
  Node* old = head->next;

  old->next->prev = head;
  head->next = old->next;

  delete old;
}

앞에서 삭제하는 함수는 어렵지 않다. 미리 삭제하는 노드를 저장해두고 그 노드를 활용해서 node들의 연결 관계를 설정해주면된다. 아마 insertFront보다는 덜 헷갈릴 것 같지만 헷갈린다면 그림을 그려서 확인하면 이해가 될 것이다.

생각보다 글이 길어지고 있어서 insertBack과 removeBack은 생략하겠다. 한 번 직접 구현해보길 권한다. 원리는 front류 함수들과 비슷하다. 사실 제일 중요한건 단순 insert와 remove이기 때문이다.

insert function

void insert(iterator iter, int e) {
  Node* v = new Node(e);

  Node* curr = iter.getNode();

  v->prev = curr->prev;
  v->next = curr;
  curr->prev->next = v;
  curr->prev = v;
}

큰 동작원리는 insertFront와 동일하다. iter.getNode()는 해당 iterator가 지시하는 노드를 가져오는 함수이다. 이 함수의 정확한 활용도는 iter node의 앞에 데이터가 e인 노드를 삽입하는 것이다.
동작원리가 유사하니 순서도 중요하게 맞춰줘야한다.

remove function

void remove(iterator iter) {
  Node* del = iter.getNode();

  del->prev = del->next;
  del->next = del->prev;

  delete del;
}

remove도 기존의 삭제 연산과 동작원리가 유사하다. 이쯤되면 약간 눈치빠른 사람들은 알 수 있는데, 삭제연산은 삽입연산에보다 좀 더 순서의 제한이 적다는 것을 눈치챌 수 있다.
이유는 간단하다. 새롭게 만들어 주는 노드는 next와 prev를 변경하는 데에 자유로운데, 앞 뒤에 연결관계가 없기때문이다.
삽입연산은 앞뒤 노드를 기준으로 새로운 연결관계를 만들어 줘야하지만 제거연산은 상대적으로 주소필드 변경이 자유로운 새 노드를 기준으로 동작되므로 삭제연산이 더 간단하다.