월요일
회귀분석 1 (Regression)
- 회귀분석 1
- 회귀분석을 하는 이유는 크게 2가지 정도로 구분할 수 있다.
- 두 변수 사이에는 선형으로 표현되는 관계가 있는가? -> 사회적관점
- 한 변수를 통해 다른 변수를 예측할 수 있을까? -> 공학적관점
- 회귀분석의 변수는 2가지가 있다. \(y = \beta_{0} + \beta_{1}x_{1} + \beta_{2}x_{2} + \epsilon\)
- 독립변수 (independent variable)
- 설명변수 (explanatory variable)이라고도 부르기도 하며 종속변수에 영향을 주는 변수이다. 위의 식에서는 $ x_1$와 $x_2 $가 독립변수이다.
독립변수가 한 개면 단순회귀, 여러 개면 다중회귀분석이 된다.
- 종속변수 (dependent variable)
- 반응변수 (response variable)이라고 부르며 관심대상이 되는 결과를 나타내는 변수다. 위의 코드에서는 $ y $가 종속변수에 해당한다.
- 회귀계수 (regression coefficient)
- 위 공식에서 $ \beta_0 , \beta_1 , \beta_2 $를 회귀계수라 부르고 곱해져있는 독립변수에대한 기울기 정도로 해석이 가능하다.
- 회귀분석을 하는 이유는 크게 2가지 정도로 구분할 수 있다.
두 변수 사이의 관계 측정도구
산점도 (scatter plot) 이전에 10주차에서 다뤘던 산점도이다. 두 변수의 대략적 관계파악에는 효과적인 도구지만 정확한 수치적 관계파악은 어렵다.
- 공분산 (covariance) \(\sigma_{XY} = \text{Cov}(X,Y) = E[(X - E(X))(Y - E(Y))]\)
두 변수 사이의 연관성과 방향은 알 수 있으나 크기의 비교가 어렵다. 상관계수 (correlation) \(\rho = \text{Corr}(X,Y)=\frac{\sigma_{XY}}{\sigma_{X}\sigma_{Y}}\)
공분산을 각각의 표준편차로 나눈 값으로 상대적인 비교가 가능하다.
이때, 상관계수는 단순회귀분석에서 회귀계수와 관련성이 높다.여기 있는 변수들의 자세한 설명은 10주차 정리본을 참고하길…
회귀분석 2 (Regression)
- 단순회귀분석 (Simple linear regression) \(Y=\beta_0 + \beta_{1}X_{1} + \epsilon\) 간단한 설명은 앞에서 했고 여기서는 $ \epsilon $이 무엇이고 무슨 역할인지를 말해보겠다.
$ \epsilon $은 오차항이라고 부르며 학부수준에서는 유일하게 회귀분석에서 확률적 성질을 갖는 값이다. 오차항 $ \epsilon$은 $i.i.d\;N(\delta, \sigma^2) $를 따른다고 가정되어있다.
여기서 $ i.i.d\; N() $는 independent and identically distribution으로 독립이면서 같은 분포인 정규분포를 말한다. 선형회귀분석에서 뿐 아니라 중회귀분석에서도 오차항의 존재로 평균선기준에서 위아래로 데이터가 분포하게 된다. - 중회귀분석 (Multiple linear regression) \(Y=\beta_0 + \beta_{1}X_{1} + \beta_{2}X_{2} + ... + \beta_{p}X_{p} + \epsilon\)
중회귀분석에서 $ Y, x_{1}, x_{2}, …, x_{p} $가 모두 확률적 성질을 갖게되면 결합분포 (joint distribution)를 활용해야하나, 학부수준에서는 x가 주어졌을 때 Y의 조건부 기댓값만을 고려하므로 확률적 성질을 갖는 것은 오차항이 유일하다.
데이터 표준화
- 데이터 표준화 \(Z = \frac{X - \overline X}{s}\) $ Y $를 설명하기 위해서 설명변수인 $ X_1, … X_p $들 사이에 variable이 크거나 하면 회귀계수의 영향력을 설명하기가 부담스럽거나 어려운 경우가 많다. 이를 해결하기 위해 데이터의 표준화 과정을 거치게 된다.
- R에서 함수는
scale(vector, center = T or F. scale = T pr F)이다. center는 위의 공식에서 $\overline X$의 유무를 결정하고 scale은 $s$의 유무를 결정한다.center = T, scale = F: $ X - \overline X $center = F, scale = T: $ X / S $
- 표준화를 하게되면 스케일이 통일되서 회귀계수에 대한 변수의 영향력이 감소된다. 결과적으로 전체적인 변수가 비슷한 범위 내에서 움직이므로 회귀계수가 클수록 강하게 Y에 영향을 줄 수 있다.
- 기존의 회귀분석 수식에서 $ \beta_0 $의 추정량이 0으로 고정된다. 따라서 절편이 없는 회귀 모형을 나타내게 된다.
- R에서 함수는
linear model function
linear model function (lm( )) 회귀분석을 구현해주는 함수가 R에서 존재한다.
lm(formula, options)의 기본 파라미터를 갖는다. formula에는 회귀모형이 들어가게 된다.
formula 작성방법
모형 formula 형식 $ y_i = \beta_0 + \beta_{1}x_{i} + \epsilon_{i}$ y~x $ y_i = \beta_{1}x_{i} + \epsilon_{i} $ y~x-1 or y~0+x $ y_i = \beta_0 + \beta_{1}x_{i1} + \beta_{2}x_{i2} + \epsilon_{i} $ y~x1 + x2 $ y_i = \beta_0 + \beta_{1}x_{i1}x_{i2} + \epsilon_{i} $ y~x1:x2 $ y_i = \beta_0 + \beta_{1}x_{i1} + \beta_{2}x_{i2} + \beta_{3}x_{i2}x_{i3} + \epsilon_{i} $ y~x1*x2 - lm( )
1 2 3 4 5 6 7 8
indy = 8 indx = 200 x = expr_dat[,indx] y = expr_dat[,indy] fit = lm(y~x) summary(fit) plot(x,y,pch=16) abline(fit,col=2,lwd=1.5)
lm()을 사용하면 회귀분석 결과 분석이 가능한 데이터를 반환해준다. 아래는 lm function 출력 결과이다.![]()
- 일단 Residuals는 한국어로는 잔차라고 하는데, $ r_i = y_i - \widehat y_i $의 값을 갖는다.
Coefficient가 있는데, 각각의 회귀 계수에 대한 가설검정 결과를 보여준다. 양측검정 결과를 보고 해당 회귀계수가 유의한지 아닌지를 결정할 수 있는데, 여기서 절편은 유의성을 보고 제외할 지 말지 결정할 때 주의를 해야한다.
위의 코드를 예로 설명을 해보면, $ Y=\beta_0 + \beta_{1}x + \epsilon $의 공식과 양측검정 결과를 확인해보면 절편은 유의하지 않고 $ \beta_1 $은 유의한 것으로 보인다.
절편이 유의하지 않은 회귀계수라고 함부로 제거할 수 있을까? 절편이 아닌 독립변수에 있는 유의하지 않은 회귀계수를 제거하는 것은 크게 상관이 없다. 하지만 절편이 유의하지 않다고해서 함부로 지우는 것은 문제가 발생할 수 있다.
만약 $ x $와 $ E(Y|x) $에서 $ x=0 $일때, 반드시 (0,0)을 지날 필요가 있다면, 절편을 제외 하는 것이 제약조건으로 들어간다. 하지만 (0,0)을 지나는 것이 의미가 없으면 유의하지 않더라도 절편은 남겨둔다.abline()에 lm함수 결과를 넣으면 lm함수의 결과를 활용해서 직선을 그려주게된다.names(fit)을 활용해서 필요한 데이터를 가져올 수 있다.- $ \beta_0 + \beta_{1}x $를 한 것을 알려주는 것이
fit$fitted.values이다.
예측값 계산
- 예측값 계산
1 2 3 4 5 6 7
pred1 = predict(fit, newdata = data.frame(x=2.3)) pred1 est = coef(fit);x1 = 2.3 y1 = est[1] + est[2]*x1 y1 pred2 = predict(fit, newdata = data.frame(x = c(1,2.2,6.7))) pred2
predict 함수를 사용하면 lm에서 사용한 formula인수의 형태에 맞춰서 신규 x값에대한 y값을 추정할 수 있다.
회귀모형 비교
- 회귀모형 비교 일반적으로 회귀분석을 할 때는 변수선택이 중요한 과정에 속하게 된다. 이를 Best subset selection이라고 하는데, 변수가 n개라고 하면 이 변수로 가능한 모든 회귀모형의 갯수는 $ 2^n $개가 된다. 그래서 변수 선택을 적당히 잘해줘야한다.
- 이 글에서는 reduced model과 full model을 비교할 것이다. full model 기준 $ Y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \epsilon $에서 $ \beta_2 x_2 $를 넣어야하는가 말아야하는가를 알아야할 필요가 있다. 두 회귀모델을 만들고
anova()함수에 넣어서 비교를 할 수 있다.
이 경우 $ H_0 : \beta_2 = 0 $이고 $ H_1 : \beta_2 \neq 0 $이다.
- 예시코드로 설명을 해보겠다.
1 2 3 4 5 6 7 8 9 10
x2 = c(1,2.2,6.7) indx = c(10,30,200) indxr = c(10,200) y = est[1]+ est[2]*x2 xf = expr_dat[,indx] xr = expr_dat[,indxr] y = expr_dat[,indy] fit1 = lm(y~xf) fit2 = lm(y~xr) anova(fit2, fit1)
anova함수 실행결과는 다음과 같다.
![]()
F-test결과로 나온 p-value를 보면 0.1912로 유의수준 0.05보다 크기때문에 위에서 제시한 귀무가설을 기각할 수 없다. 이거는 결과적으로 해석해보면 회귀계수 $ \beta_2 $가 0이어도 전체적인 회귀모델에는 크게 상관이 없다고 볼 수 있다.
- 문자열로도 회귀모델을 비교할 수 있다.
1 2 3 4 5 6 7 8 9 10 11
ftxt = paste0(uq_names[indy], '~', paste0(uq_names[indx], collapse="+")) ftxtr = paste0(uq_names[indy], '~', paste0(uq_names[indxr], collapse="+")) ftxt ftxtr colnames(expr_dat) = gsub("[ .]","",uq_names) lm_dat = data.frame(expr_dat) fit1 = lm(as.formula(ftxt), data=lm_dat) fit2 = lm(as.formula(ftxtr), data=lm_dat) anova(fit2, fit1)
위의 코드 출력결과는 아래와 같다.
![]() 여기서 이제 p-value가 역시나 축소모형을 지지하므로 ANXA8은 모형에서 제외해도 큰 상관이 없음을 알 수 있다.
여기서 이제 p-value가 역시나 축소모형을 지지하므로 ANXA8은 모형에서 제외해도 큰 상관이 없음을 알 수 있다.
사실 위의 코드는 첫번째 예시 코드와 동일한 코드이다. 단지 formula 해석의 편의성이 문자열로 작성하면 훨씬 편리해지는 것을 알 수 있다.
- 이 글에서는 reduced model과 full model을 비교할 것이다. full model 기준 $ Y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \epsilon $에서 $ \beta_2 x_2 $를 넣어야하는가 말아야하는가를 알아야할 필요가 있다. 두 회귀모델을 만들고
모형진단 - 오차항의 가정
- 오차항 가정
오차항의 등분산성 $ (\widehat y_i, e_i) $의 산점도를 활용한다. 등분산성이란 $ e_i $를 기준으로 데이터가 얼마나 균일한 간격으로 퍼져있는 지를 말한다.
여기서 $ e_i$는 잔차로 $r_i = y_{i} - \widehat y_{i} $이다.오차항의 독립성 잔차를 사용해서 패턴이 존재하는 지를 확인한다. 만약 데이터를 봤는데, 패턴이 존재하면 오차항이 독립적이지 않을 경우가 많다. 그래서 패턴이 있는 지 없는 지를 확인해야한다.
- 오차항의 정규성 x축을 정규분포의 quantile로, y축 자료의 quantile로 두고 점을 찍어봤을 때, 직선에 가깝게 나올 경우 데이터가 정규분포를 따른다고 볼 수 있다.
- 잔차의 산점도 예제
1 2 3 4
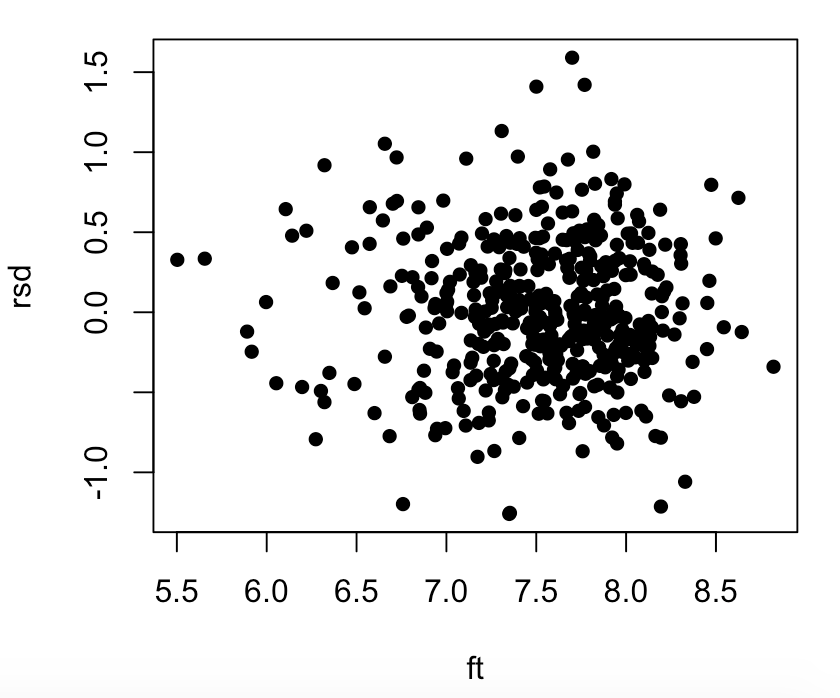
rsd = resid(fit2) # resid return e ft = fitted(fit2) # fitted return y_hat plot(ft, rsd, type = 'p', pch=16) hist(rsd, breaks=20)
실행결과를 보면 아래와 같다.
![]()
![]() 히스토그램을 보면 정규분포를 따름을 알 수 있고, 산점도를 보면 패턴이 있다고 보기는 어렵다.
히스토그램을 보면 정규분포를 따름을 알 수 있고, 산점도를 보면 패턴이 있다고 보기는 어렵다. - QQ plot
1 2
qqnorm(rsd) qqline(rsd, col=2, lwd=2)
잔차의 qq plot을 찍어보면 아래와 같이 나오게 된다. 당연히 위에서 정규분포를 따름을 확인했으므로 qq plot은 직선을 띄게 된다.
![]()



 여기서 이제 p-value가 역시나 축소모형을 지지하므로 ANXA8은 모형에서 제외해도 큰 상관이 없음을 알 수 있다.
여기서 이제 p-value가 역시나 축소모형을 지지하므로 ANXA8은 모형에서 제외해도 큰 상관이 없음을 알 수 있다.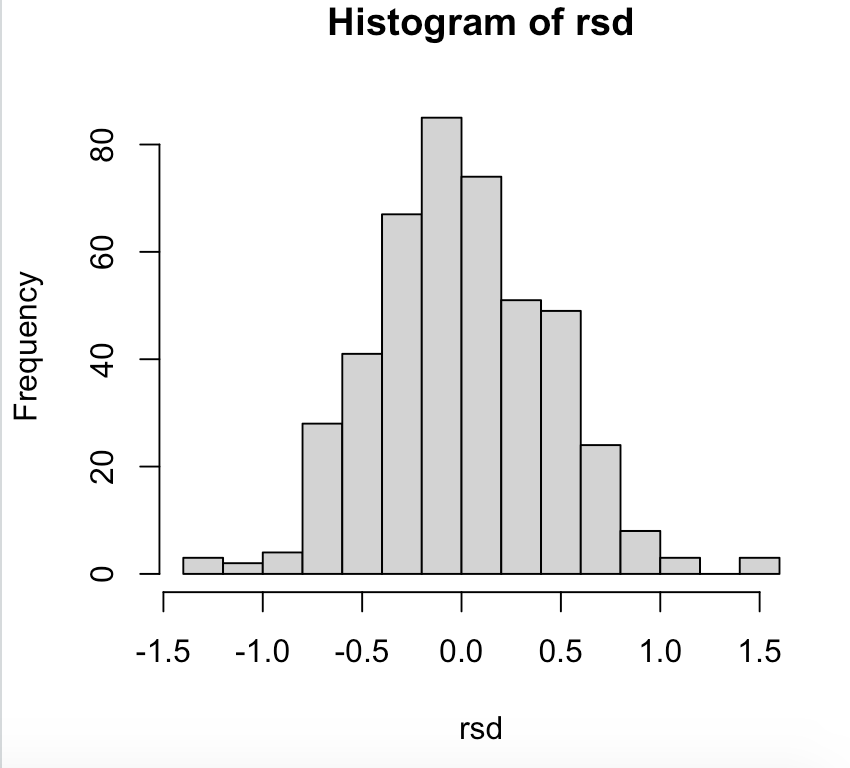
 히스토그램을 보면 정규분포를 따름을 알 수 있고, 산점도를 보면 패턴이 있다고 보기는 어렵다.
히스토그램을 보면 정규분포를 따름을 알 수 있고, 산점도를 보면 패턴이 있다고 보기는 어렵다. 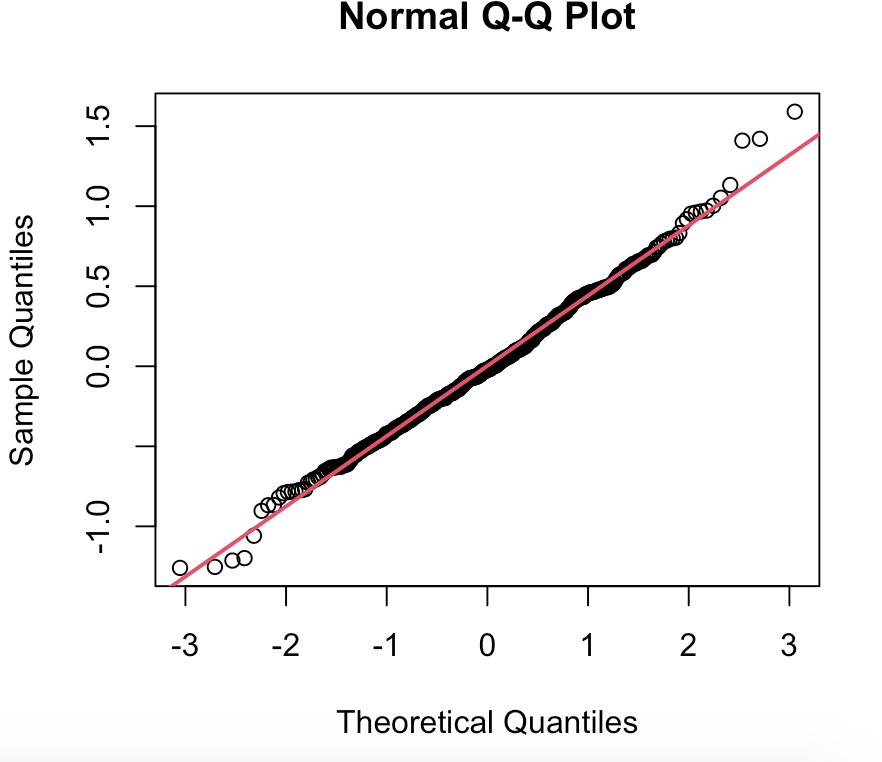
Comments powered by Disqus.