월요일
분포함수
- 분포함수
- 일반적으로 분포함수를 사용하는 방법은 (키워드 + 분포이름)의 형식으로 사용한다.
키워드는 다음과 같이 종류가 있다.- d : Density function (밀도 함수)
- q : Quantile function (분위수 함수)
- p : Cumulative Density function (누적밀도함수)
- r : Generate Random Numbers from such distribution (난수 형성)
- 일반적으로 분포함수를 사용하는 방법은 (키워드 + 분포이름)의 형식으로 사용한다.
정규분포함수 (Normal distribution)
- 정규분포함수
dnorm(x, mean=m, sd=s)
dnorm()은 $ X \sim N(m, s^2) $을 따르는 정규분포 곡선의 함수를 $ f(x) $라 하면, 해당 함수의 x에 해당하는 값을 반환해준다.
qnorm(x, mean=m, sd=s)는 $ X \sim N(m, s^2) $을 따르는 정규분포 곡선에서 $ \text{P}(\text{X} \leq x)=\text{x} $인 $ x $를 반환해준다. 쉽게 말하면 정규분포확률에 해당하는 값을 반환해준다.
pnorm(x, mean=m, sd=s)는 $ X \sim N(m, s^2) $를 따르는 정규분포곡선에서 $ \text{P}(\text{X} \leq x) = F(x)$라 할때, $ F(\text{x}) $를 반환해준다.rnorm(num, mean=m, sd=s)는 $ X \sim N(m, s^2) $인 정규분포 내에서 num개만큼의 난수를 만들어준다.
균일분포함수 (Uniform distribution)
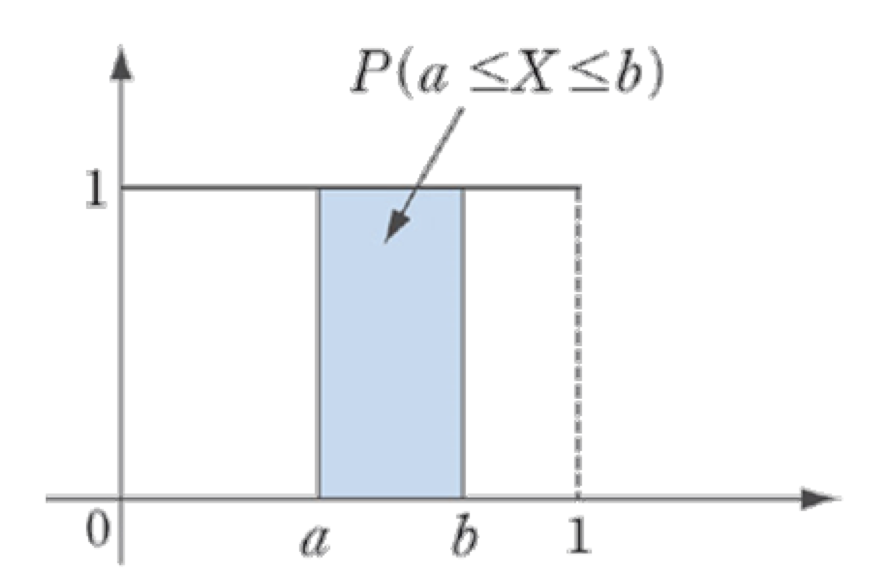
균일분포함수 우선 균일분포란, 아래와 같이 $ p(x) $의 그래프가 정의된 구간에서 같은 높이로 주어지는 분포를 말한다. 일반적으로 구간 $ \theta_1, \theta_2 (\theta_1 < \theta_2) $에서 정의된 경우, $ U(\theta_1, \theta_2) $로 나타낸다.
![unif]()
좀 더 수식적으로 접근을 하면 다음과 같다.
\(if\;\;\text{X}\sim U(a,b),\;\; Let\;f(x)=c\) \(\int_{a}^{b}f(x)dx=1\) \(\therefore c=\frac{1}{b-a}\)
위의 이미지로 설명예시를 하겠다.dunif(x, min=0, max=1)는 그림과 같이 균일분포가 주어졌을때, x의 함수값을 알려준다. 즉 쉽게 말하면dunif는 위의 수식에서 $ c $ 값을 반환해준다고 생각하면된다.
qunif(x, min=0, max=1, lower.tail=T or F)는 분위수를 계산해준다. 이때, lower.tail의 값에따라 분위수가 바뀌는데, 누적분포함수(CDF, Cumulative Distribution Function)를 활용해서 분위수를 계산한다.
lower.tail=T이면 $ \text{P}(\text{X}\leq x) $의 확률값을 반환해주고lower.tail=F이면 $ \text{P}(\text{X} > x) $의 확률값을 반환해준다.
punif(x, min=0, max=1, lower.tail=T or F)는 $ \text{F}(x) $를 CDF라하면,lower.tail=F일때는 $ 1-\text{F}(x) $를 반환해준다.lower.tail=T이면 CDF 그 자체를 계산해준다.runif(num, min, max)는 $ [min, max] $의 정의역 범위에서 num개의 난수를 만들어준다.
초기하분포 (Hypergeometric distribution)
초기하분포
![hyper]()
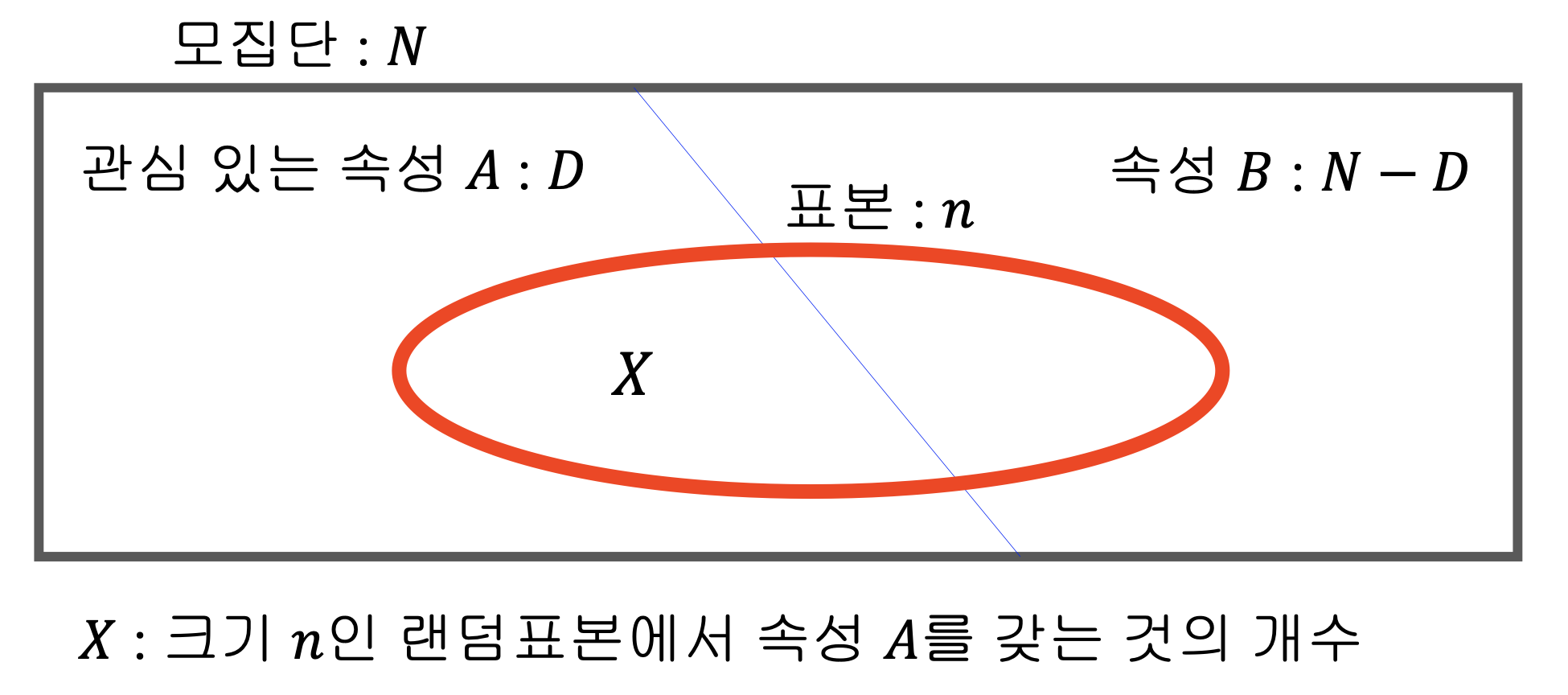
초기하분포란, N개의 특성값으로 이루어진 유한모집단이 두가지 속성만 갖는다. 관심속성을 갖는 특성값이 전체 N개 중에서 D개 포함되어 있다고 할 때, N개 중에서 n개의 표본을 추출하여 관심속성의 특성값이 나오는 수의 분포를 말한다.
수식으로는 아래와 같이 나타낼 수 있다.\(\text{X}\sim HG(N, D, n) \text{ means}\) \(\text{P}(\text{X}=x)=P(x) = \frac{(_{\;x}^{D})(_{\;n-x}^{N-D})}{(_{n}^{N})}\)
사실 이게 이렇게 말하면 어려워보이는데 흔히 자주 보는 확률문제랑 똑같다. 이런 유형의 대표적인 문제가 다음과 같다.
ex) 주머니 속에 흰 공 5개, 검은 공 3개가 있다. 주머니에서 공3개를 비복원 추출로 꺼낼 때, ~~~- 흰 공이 x개일 확률은? :
dhyper(x, D, N-D, n, log=T or F)는 $ HG(N, D, n) $일때, $ P(\text{x}) $와 같다. - 흰 공이 x개 이상일 확률은? :
phyper(x, D, N-D, n, lower.tail = T or F, log.p=T or F)는 누적분포를 계산해준다. 역시나 lower.tail의 역할은 동일하다. - 비복원 추출로 공을 뽑은 확률이 p일때, 몇 번 추출했는가? :
qhyper(p, D, N-D, n, lower.tail = T or F, log.p = T or F)는dhyper의 반대동작으로 생각하면 된다. 특정확률이 나오기 위해서는 몇번의 추출이 이뤄지는 지를 알아내준다. rhyper(nn, D, N-D, n)는 해당 초기하분포를 기반으로 nn번 모의 실험을 진행하는 것이다. nn값이 클수록 rhyper로 나온 값으로 확률 계산을 하면 dhyper에 수렴한다.
- 흰 공이 x개일 확률은? :
이항분포 (Binomial distribution)
이항분포 이항분포는 베르누이시행 (독립시행)을 반복하여 관심사건이 몇 번 나왔는 지를 활용한 확률분포다.
수식으로 표현하면 다음과 같다.\(\text{if}\;\text{X}\sim B(n,p)\) \(p(x) = (_{x}^{n})p^x(1-p)^{(n-x)}\) \(\sum_{x=0}^{n}p(x)=\sum_{x=0}^{n}(_{x}^{n})p^x(1-p)^{(n-x)} = (1+(1-p))^n=1\)
dbinom(x, n, p, log =F or T)는 $ p(\text{x}) $값을 구해준다.pbinom(x, n, p, lower.tail = T, log.p)는 $ P(\text{X} \leq \text{x}) $와 같다.qbinom(p, n, p, lower.tail = T, log.p)는 역시나 dbinom의 반대 과정이다.rbinom(nn, n, p)은 역시나 모의추출로 난수형성이다.
카이제곱분포 (Chi-squared distribution)
카이제곱분포 카이제곱분포(chi-squared distribution)는 정규분포와 관련이 깊다. k개의 서로 독립적이고 표준정규분포를 따르는 확률변수 X를 제곱한 값들을 합하였을 때 분포이며 k는 자유도라고하고 카이제곱분포의 parameter역할을 하게된다. 보통 독립성 검정을 할 때 사용하고 모집단의 분산에 대한 추정과 검정을 할 때 사용한다.
아무래도 분산비교를 하는 분포다보니 전체적인 분포의 형태는 F-분포의 형태를 띄게 된다. 자유도라는 개념이 참 와닿지는 않는데, 검색하다가 괜찮은 예시가 있어서 가져왔다.‘자유도’를 아주 간단한 예를 들어 설명하자면, 5개의 숫자 평균이 3이라고 해봅시다. 이 때 5개 중 4개의 숫자는 마음대로 고를 수 있지만, 마지막 1개의 숫자는 반드시 정해져 있습니다. 이런 경우에 자유도가 4라고 합니다.
수식으로 나타내면 아래와 같다.
\(V = {Z_1}^2+{Z_2}^2+{Z_3}^2+...+{Z_k}^2 \Rightarrow V \sim \chi^2(k)\) \(E(V) = k,\quad Var(V)=k^2\) \(\frac{\sigma^2}{(n-1)s^2}\sim\chi^2(n-1)\)
함수 사용법은 나머지 함수들과 동일한데, 좀 다른 parameter가 추가적으로 있다. ncp라는 parameter인데, Non centrality parameter로 평균이 0이 아닌 경우에 처리를 해주는 parameter이다.
(사실 카이제곱분포는 무슨 말인지 아직도 잘 안 와 닿는다… 그래서 차마 설명을 못적겠다.)
t-분포 (Student’s t-distribution)
- t-분포 t분포는 일반적인 상황에서 정규분포계산을 위해서 존재하는 분포이다. 정규분포에서는 일반적으로 모분산($ \sigma^2 $)을 알고있다고 가정한다. 하지만 현실은 모분산을 알이 위해서 표본추출을 진행하는데, 이때 표본분산($ s^2 $)이 사용된다. 이 경우에는 표준정규분포인 z값을 사용할 수 없기때문에 표본확률분포 중 하나인 T-통계량인 t-분포를 사용한다.
자유도를 모수로 갖고있기 때문에 자유도가 높을수록(=표본의 수가 많을수록) 중심극한의 정리에 의해서 정규분포에 근사하게 된다. 수식은 보통 아래와 같이 나타낸다.
\(Z\sim N(0,1),\; V\sim\chi^2(k),\;Z\text{ and }V\text{ is independent}\) \(\Rightarrow T=\frac{Z}{\sqrt{V/k}}\sim t(k)\)dt(x, df, log=F or T)는 일반적인 t-분포의 값을 보여준다. 여기서 df는 degrees of freedom으로 자유도를 나타낸다. 즉 표본 갯수를 말해준다. 기본적으로 t-분포는 정규분포의 틀을 가지고 있기때문에 함수들의 반환값은 norm function과 유사하게 해석이 가능하다.
F-분포 (F-distribution)
- F-분포 F-분포는 두 정규모집단의 분산을 비교할 때 사용하는 분산 분석에 사용한다. 수식은 다음과 같다.
\(V_1\sim\chi^2(k_1),\quad V_2\sim\chi^2(k_2),\quad V_1,V_2 \text{ is independent}\) \(\Rightarrow F=\frac{V_1/k_1}{V_2/k_2}\sim F(k_1,k_2)\) \(\text{ : F-distribution with degrees of freedom }(k_1,k_2)\)df(x, df1, df2, log=F or T)의 형태로 사용된다. 카이제곱분포와 함께 아직 이해가 안되는 분포이다. 그나마 카이제곱분포보다는 이해가 되는데, 일단은 어디에 쓰이는 지는 이해가 된다.
분산분석이란 일반적으로 문제를 위해서 만들어진 정규분포는 평균이 다르고 분산값이 같은 경우가 많았다. 하지만 현실의 데이터는 평균도 다르고 분산도 다를 수 밖에 없다. 분산이 다르게 될 경우 두 모집단을 비교하기가 어렵다. F-분포 식을 보면 두 집단의 분산을 나누는 것을 알 수 있는데, F-분포 그래프를 그렸을때, 1 부근의 값이 많이 나올수록 서로 비슷하거나 연관성이 있다고 보게 된다.
중심극한정리 (Central Limit Theorem)
- 중심극한정리
1 2 3 4 5 6 7 8 9 10 11 12 13
df = 4 niter = 1000 xm <- rep(0, niter) for (i in 1:niter) { X <- rchisq(100, df=4) xm[i] = (mean(X)-4)/(sqrt(2*4)/sqrt(100)) } hist(X, breaks=20, main = expression(chi^2~(4)), col = 'lightblue') x11() hist(xm, breaks=20, main = expression(over(bar(X)-mu, sigma/sqrt(n))),col = 'gray', xlab='normalized sample mean')
- 가설검증 시에 굉장히 중요한 이론이다. 정규분포관련 공부할 때 가장 많이 언급되는 말이 있다.
표본평균들의 분포는 정규분포를 이룬다.
이 말이 곧 중심극한정리를 한 문장으로 요약한 것이다.
- 코드를 간단하게 설명을 해보자. niter는 총 사용되는 표본평균 갯수이다. 이때, 표본평균은 자유도가 4인 카이제곱분포를 100개 모의추출로 활용한다. xm에 들어가는 값은 $\frac{\overline{X}-\mu}{\sigma/\sqrt{n}}$가 되게 된다.
- 가설검증 시에 굉장히 중요한 이론이다. 정규분포관련 공부할 때 가장 많이 언급되는 말이 있다.
목요일
가설검정이론
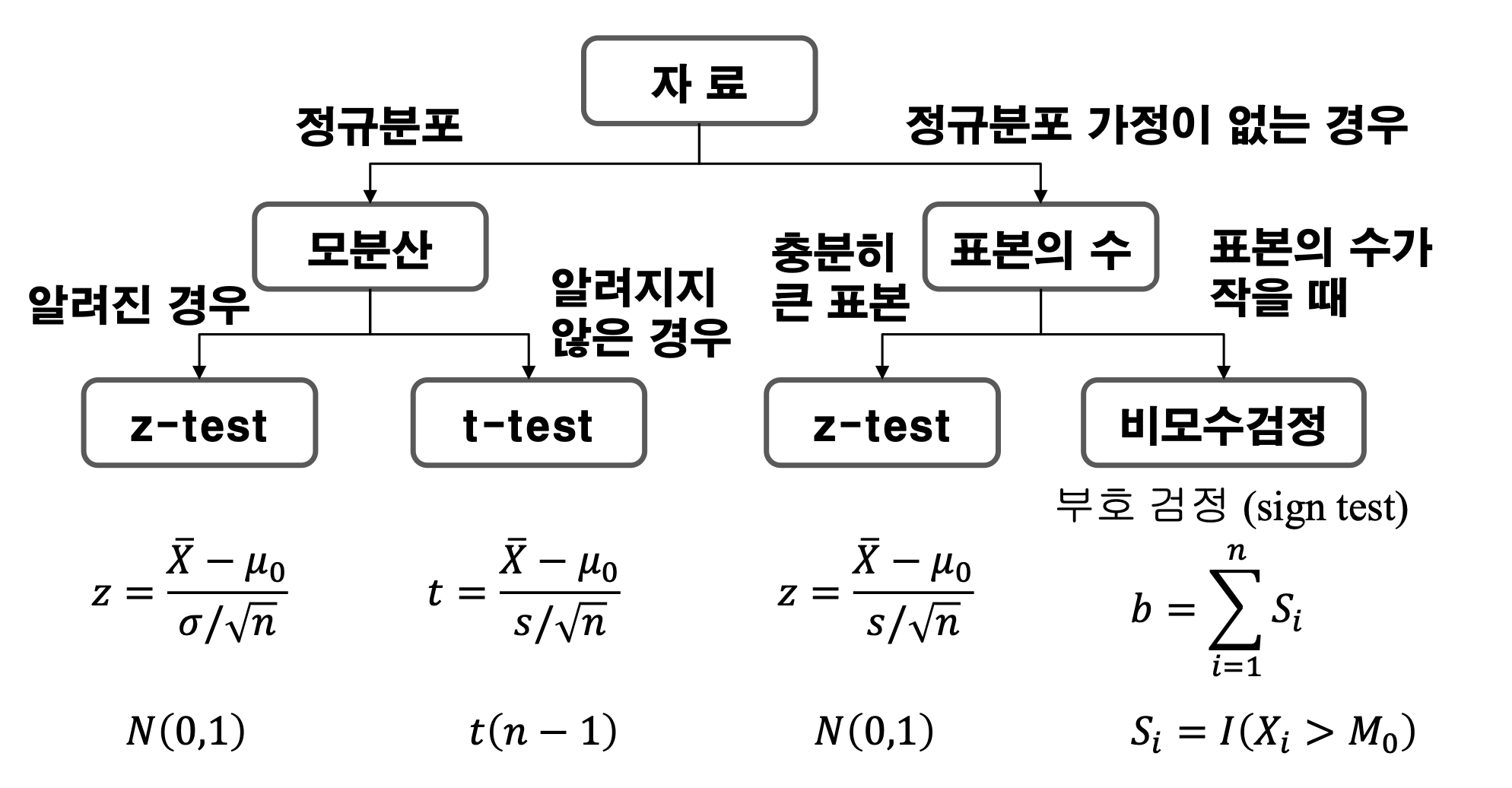
- 가설검정이론 \(H_0 : \mu = \mu_0\text{ (Null hypotheis)}\) \(H_1 : \mu = \mu_1\text{ (Alternatice hypothesis)}\)
- 통계학에서는 어떤 상황을 판단할 때, 가설을 세우고 가설검정을 진행한다. 이때 가설은 보통 2가지가 있는데, 귀무가설($ H_0 $, Null hypothesis)과 대립가설($ H_1 $, Alternative hypothesis)가 있다. 대립가설은 검정과정을 통해 귀무가설이 기각된 것을 확인하면 대립가설이 채택된다.
- 통계학 수업의 전반적인 흐름은 크게 3가지로 나눠진다.
- 모집단
- 표본
- 추정
모집단을 공부하면서 전체 데이터의 정보를 다루게 되고, 표본 과정을 통해 표본 데이터를 다루는 법을 배운다. 모집단의 데이터를 알기 위해서 통계학적 계산을 하므로 표본으로 얻은 데이터를 통해 모집단을 추정하게 된다.
- 추정과정에서 가설이 필요한 이유는 간단히 말하면 우리가 가진 표본평균이 정확한 값이 아니기 때문이다. 표본을 배울 때 가장 먼저 배우는 것 중 하나가 바로 표본평균($ \overline X $)이다. 물론 표본평균의 평균은 모평균의 평균과 같지만 각각의 표본평균은 실제 모평균과 다른 값들을 갖게된다. 즉 표본평균은 일종의 변수인 것이다. 표본평균을 평균이라고 두고 가설검정을 하게 되면 기준점이 너무 불안정하기 때문에 경우에 따라서 대립가설의 기각 여부가 달라진다. 그래서 우리는 $ \mu = \mu_0 $라고 가정을하고 가설검정을 하게된다.
- 그렇다면 왜 귀무가설의 기각여부를 확인하는 것일까?
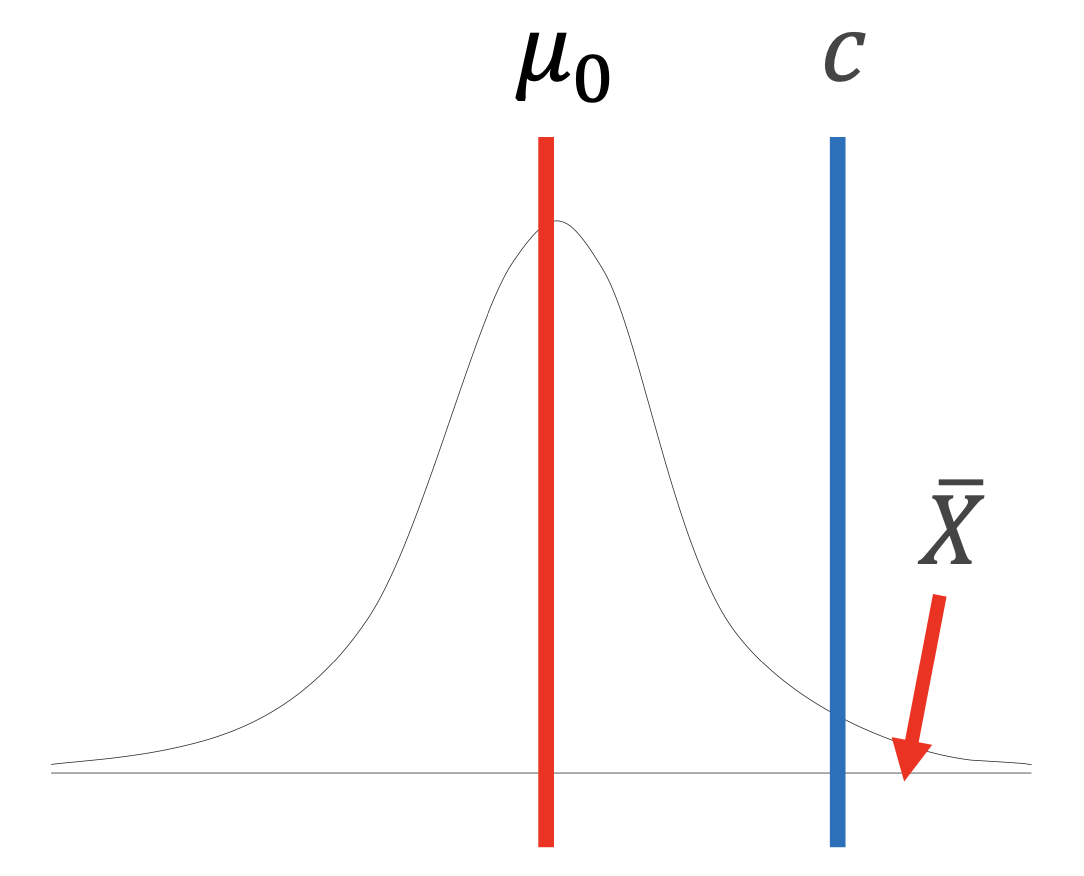
![hypo]()
위의 그래프에서 표본평균들이 정규분포 상에서 굉장히 확률이 낮은 구간에서 포착이 되었을 때, “이 가설이 맞을 가능성이 낮다”고는 확실하게 말할 수 있다. 하지만 과연 $ \mu_0 $에 가깝다고 이 가설이 맞을 가능성이 높다고 단정하기는 어렵다.
왜냐하면 사실 $ \mu_0 $도 결국에는 가설로 세운 정확하지 않은 수치 값이다. (모든 표본을 다 조사하는 건 현실에선 불가능 하니까… 그리고 일반적으로는 모평균에서 약간의 차이를 가진 값으로 보는 것 같다.)
만약, 우리가 대립가설로 세운 $ \mu_1 $에 우연하게 표본평균들이 가깝게 나온다면 그것만으로 확실하게 귀무가설이 틀렸다고 할 수 있을까? 아마 쉽게 단정짓기는 어려울 것이다. 보통은 대립가설이 귀무가설이 아니다~ 라는 식으로 흘러가기 때문에 좀 더 실질적으로는 이해가 어려운 편은 아니다.
그래서 가설검정에서 보통 귀무가설이 틀린 강한증거 라는 방향으로 얘기를 하게된다.- 가설검정 조합 종류는 아래와 같다. \(\text{단순가설 vs 단순가설}\) \(H_0 : \mu=\mu_0,\quad H_1 : \mu = \mu_1\) \(\text{}\) \(\text{단순가설 vs 복합가설}\) \(H_0 : \mu=\mu_0,\quad H_1 : \mu \neq \mu_0\quad(H_1 : \mu > \mu_0)\) \(\text{}\) \(\text{복합가설 vs 복합가설}\) \(H_0 : \mu \leq \mu_0,\quad H_1 : \mu > \mu_0\)
제일 마지막의 두 조합은 2번째 조합으로 대치할 수 있음이 알려져있다.
오류 (error)
- 오류
- 제 1종 오류 (type I error, \(\alpha\) ) : $ \text{P}(H_{0}기각 | H_{0}사실) $
- 제 2종 오류 (type II error, \(\beta\) ) : $ \text{P}(H_{0}기각 | H_{1}사실) $
![error]()
단측, 양측검정
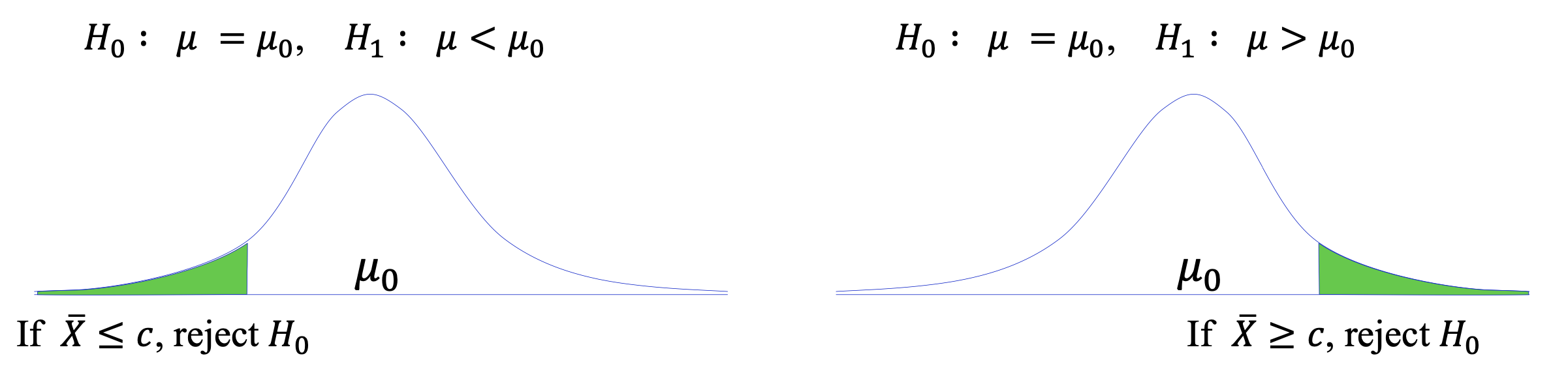
단측검정 (one-sided text)
![one]()
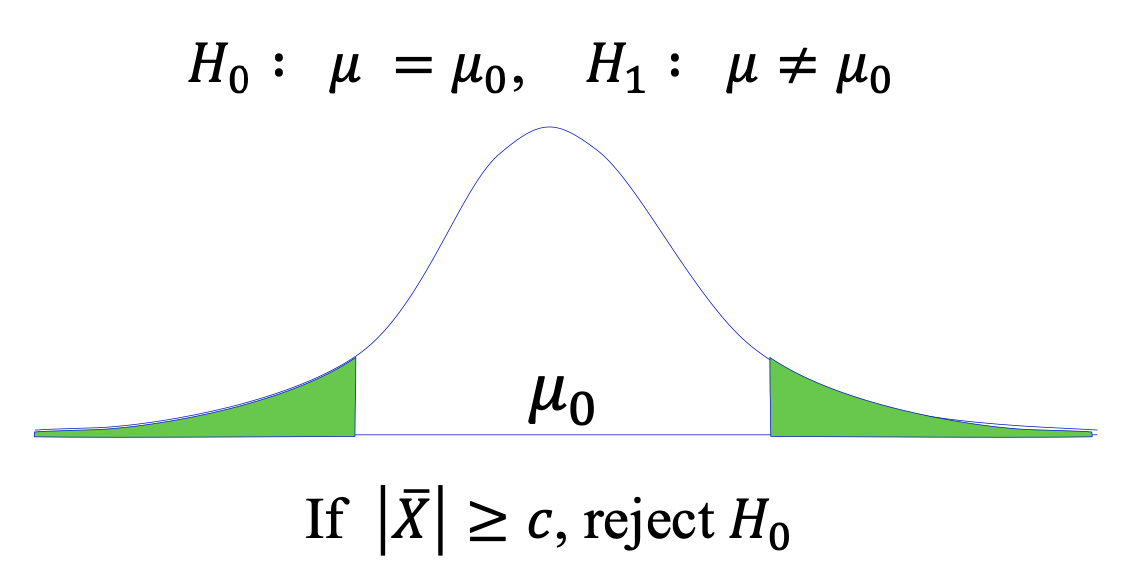
양측검정 (two-sided text)
![two]()
검정통계량
- 검정통계량 \(z = \frac{\overline X - \mu_{0}}{\sigma / \sqrt{n}}\approx N(0,1)\) \(\text{}\) \(t = \frac{\overline X-\mu_0}{s/\sqrt{n}}\sim t(n-1)\)
z-통계량은 정규화가 된 상태에서 표준정규분포에 적용해서 검정할 때 사용하고, t-통계량은 분산을 모를 때 사용하는 것이다.
임계값과 p-value
임계값 임계값은 기각역을 지정해주는 값이 된다. 보통 검정통계량이 임계값에 들어가게 된다.
유의확률 (p-value) 유의확률은 검정통계량으로부터 계산되어 나온 값이다. 분포 그래프에서 검정통계량을 이용해서 대립가설을 지지하는 방향으로 나올 확률을 말한다. 즉 기각이 되었을 때 어느정도 수준으로 기각을 하는 지를 말해준다. 귀무가설이 신뢰구간을 벗어날 확률이다.
가설검정코드
- 가설검정코드
1 2 3 4 5 6 7 8 9 10
t1 = t.test(expr_dat[,1], mu=7, conf.level = 0.95, alternative = "two.sided") t2 = t.test(expr_dat[,1], mu=6.5, conf.level = 0.95, alternative = "less") t3 = t.test(expr_dat[,1], mu=6.5, conf.level = 0.95, alternative = "greater") t1; t2; t3
t-검정을 하는 함수이다.
alternative = c("two sided", "less", "greater")로 각각 수식으로는 다음과 같다.
“two sided” : $H_1 : \mu \neq m_0$
“less” : $\mu < \mu_0$
“greater” : $\mu > \mu_0$- 여기서 나름 중요한 부분은 conf.level 파라미터이다. 생긴 것 그대로 신뢰구간(confidence level)을 정해주는 것인데, 이게 왜 중요하냐면 t-분포를 활용한 검정에서는 유의수준($\alpha$)을 활용한다. 유의수준이란, 제 1종 오류를 범할 확률의 최댓값을 말하며 일반적으로 $\alpha$값은 5%나 1%를 사용한다. 보통 1종 오류를 2종 오류보다 심각하게 다룬다. 억울한 죄인을 만들 수 있기때문이다.
(이 말은 가설검정을 진행할 때, 결과가 이 정도까지 벗어나면 귀무가설이 오류라고 인정하는 수준이다.)
근데 신뢰구간 공식은 (1-$\alpha$)%로 정의되므로 신뢰구간과 유의수준은 직접적인 연관성이 존재한다.
위의 코드를 실행한 결과를 보고 해석하는 방법을 말해보자.
![t1]()
t1을 실행하면 위처럼 나오는데, 하나 하나 뜯어보겠다. 해석을 위한 데이터의 이름 은 expr_dat[,1]이다. 데이터들을 이용해서 계산한 t-통계량 값은 0.39073이고 자유도(df, degrees of freedom) 는 441이다.
그 다음에 나오는 값이 p-value 인데, p-value는 귀무가설을 잘못 기각할 확률을 말하기 때문에 p-value가 유의수준보다 작으면 귀무가설을 기각한다. 이게 좀 헷갈리는데 쉽게 말하면 p-value가 5%라는 것은 내가 귀무가설을 기각하는 게 틀릴 확률이 5%라고 계산되어 나온 것이다! 즉 내가 아무렇게나 기각해버려도 5%정도 틀린다는 것이다.
결과적으로 p-value가 유의수준 5%보다 크기 때문에 기각할 수가 없다. 결과 값에서 95% 신뢰구간을 보면 [6.968453, 7.047203]이므로 이 구간 내에 평균치가 존재하므로 기각이 어렵다. 그리고 mean of x는 흔히 말하는 $\overline x$이다.(사실 아직도 잘 모르겠다.)
두 집단간의 모평균 가설 검정
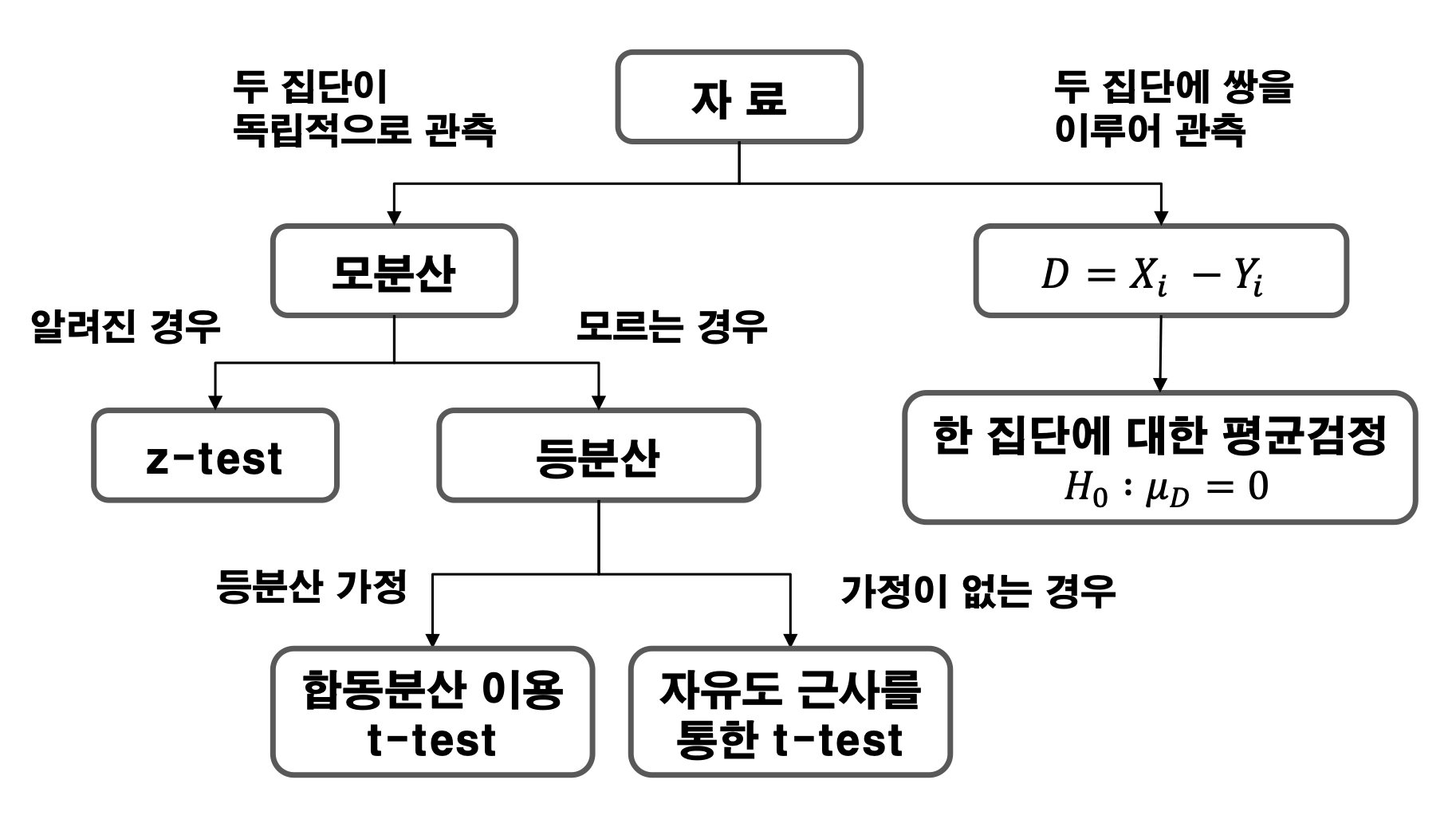
- 두 집단간의 가설 검정 \(H_0 : \mu_1 = \mu_2\text{ (Null hypotheis)}\) \(H_1 : \mu_1 \neq \mu_2,\quad \mu_1 > \mu_2,\quad \mu_1 < \mu_2\text{ (Alternatice hypothesis)}\)
두 집단에 대한 분석을 진행할 경우에는 두 집단이 독립적인지 쌍으로 이루어진 것인지 확인할 필요가 있다. pair를 이루는 경우는 두 표본평균의 차를 활용해서 검정을 진행한다.
쌍을 이룬다는 의미가 무엇이냐면 대표적인 예시로는 어떤 약을 먹기 전과 먹은 후의 변화 같은 경우가 쌍을 이룬 데이터다.
두 집단 가설검정 코드
- 두 집단 가설검정 코드
1 2 3 4 5 6 7 8 9 10 11 12
n=25 x=rnorm(n, mean=1, sd=1) y=x+rnorm(n, mean = 0.5, sd=1) t1 <- t.test(x,y,alternative = "two.sided",paired = T, var.equal = F) t2 <- t.test(x,y,alternative = "less",paired = T,var.equal = F) t3 <- t.test(x,y,alternative = "greater",paired = T, var.equal = F) t1;t2;t3
paired 변수를 설정해주면 해당 데이터가 쌍을 이루는 지 아닌 지를 알 수 있다.



Comments powered by Disqus.