월요일
상자그림 (boxplot)
- boxplot
1 2 3 4 5 6 7 8 9
mat = expr_dat[,c(3,4,7,8)] x11() install.packages("gplots") library(gplots) boxplot(mat,col=rainbow(4,alpha=0.6)) res = boxplot(mat,plot=F) res$out[res$group==1]
![boxplot]()
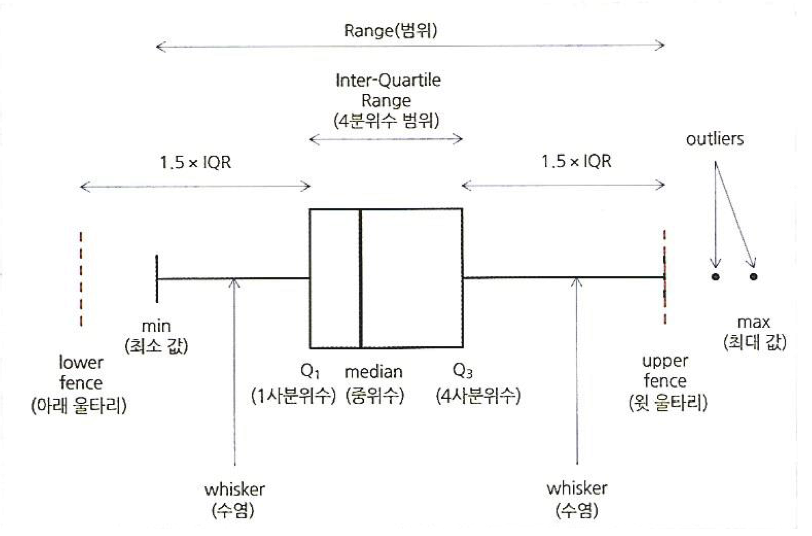
- 상자그림이란 자료의 분포를 한눈에 보여주는 그래프이다. 이상점(outlier), 사분위수(Quartile), 중위수(median) 등 데이터셋의 정보를 한눈에 볼 수 있다.
- 간단하게 상자그림을 설명해보면…
- 그림 상의 사각형 상자는 1분위수($Q_1$)~4분위수($Q_3$)까지를 보여준다. 이때 1분위수는 25% 데이터, 4분위수는 75% 데이터를 보여준다.
- 상자 내부의 검은 선은 중위수(median)로 해당 데이터 셋의 정확히 50%위치의 값을 보여준다.
- 상자로부터 위아래로 뻗은 직선(수염 이라고 한다.)은 최대와 최소까지의 범위를 표현해준다. 만약 최대와 최소가 각각 $Q_3 + 1.5IQR, Q_1 - 1.5IQR $ 범위 안에 있다면, 해당 값까지만 표시해주면 된다. 하지만 그 범위 밖의 값이 존재한다면 수염을 $1.5IQR$ 범위까지 표현해주고 그 이 후는 점을 찍어서 해당 값들은 이상점(outlier)으로 표시해준다.
- boxplot은 gplots 패키지에 있다.
- plot이 True (default)라면 상자그림이 생성이 되고 상자그림을 그리기 위한 필요 정보들이 반환된다. False값이면 상자그림은 반환되지 않고 필요정보만 반환된다.
선그림 (plot)
- plot
1 2 3 4 5
pop_dat = read.csv(file = 'table_2_2.csv') x11() plot(pop_dat[,1],pop_dat[,2],type = 'l',xlab='연도',ylab = '인구수') plot(pop_dat[,1],pop_dat[,2],type = 'b',xlab='연도',ylab = '인구수')
- 일반적인 선그래프를 그려주는 함수이다. boxplot과 마찬가지로 gplots패키지에 있으며 함수 작동 형식은
plot(x, y, type, other options)이다. - type은 크게 2가지 종류가 있다. type이 ‘l’이면 lines only의 의미로 선만 표시해준다. type이 ‘b’면 both points and lines의 의미로 선과 데이터의 점을 모두 표시해준다.
- 일반적인 선그래프를 그려주는 함수이다. boxplot과 마찬가지로 gplots패키지에 있으며 함수 작동 형식은
산점도 (scatter plot)
- scatter plot
1 2 3 4 5 6 7 8 9 10
ind1=8; ind2=12 plot(expr_dat[,ind1], expr_dat[,ind2], type='p', pch=16, xlab=uq_names[ind1], ylab = uq_names[ind2]) cor_mat = cor(expr_dat) which.max(cor_mat[ind1,-ind1]) ind1=8; ind2=200 plot(expr_dat[,ind1], expr_dat[,ind2], type='p', pch=16, xlab=uq_names[ind1], ylab = uq_names[ind2])
데이터의 관계를 볼 수 있는 그래프이다. 두 변수 사이의 상관관계를 확인해야하는데, 이때 산점도 그래프를 확인해볼 가치가 있다. 인공지능 공부에서 선형회귀에서 경사하강법을 사용 할 때 데이터의 방향성을 산점도 그래프의 형태로 확인하는 경우가 있다. 데이터의 전체적인 형태가 직선을 띌수록 두 변수의 상관관계가 높다. 참고록 pch가 16이면 채워진 원으로 표시해준다.
산점도 행렬 (scatter plot matirx)
- scatter plot matrix
1 2 3 4
ind = c(2,8,12,200) pairs(expr_dat[,ind]) pairs(expr_dat[,ind], "Expression Data", pch = 21, bg = c("red","blue")[gr_ind])
산점도 그래프는 두 변수의 관계를 보여준다. 하지만 우리가 다루고 있는 데이터인 Expr_dat처럼 여러가지의 변수가 존재하는게 제일 일반적인 데이터 셋이다. 그래서 우리가 원하는 데이터들의 조합으로 산점도 그래프들을 모아서 보는 것이 편하다. 이때 사용하는 것이 산점도 행렬을 만들어주는 함수인
pairs()이다.
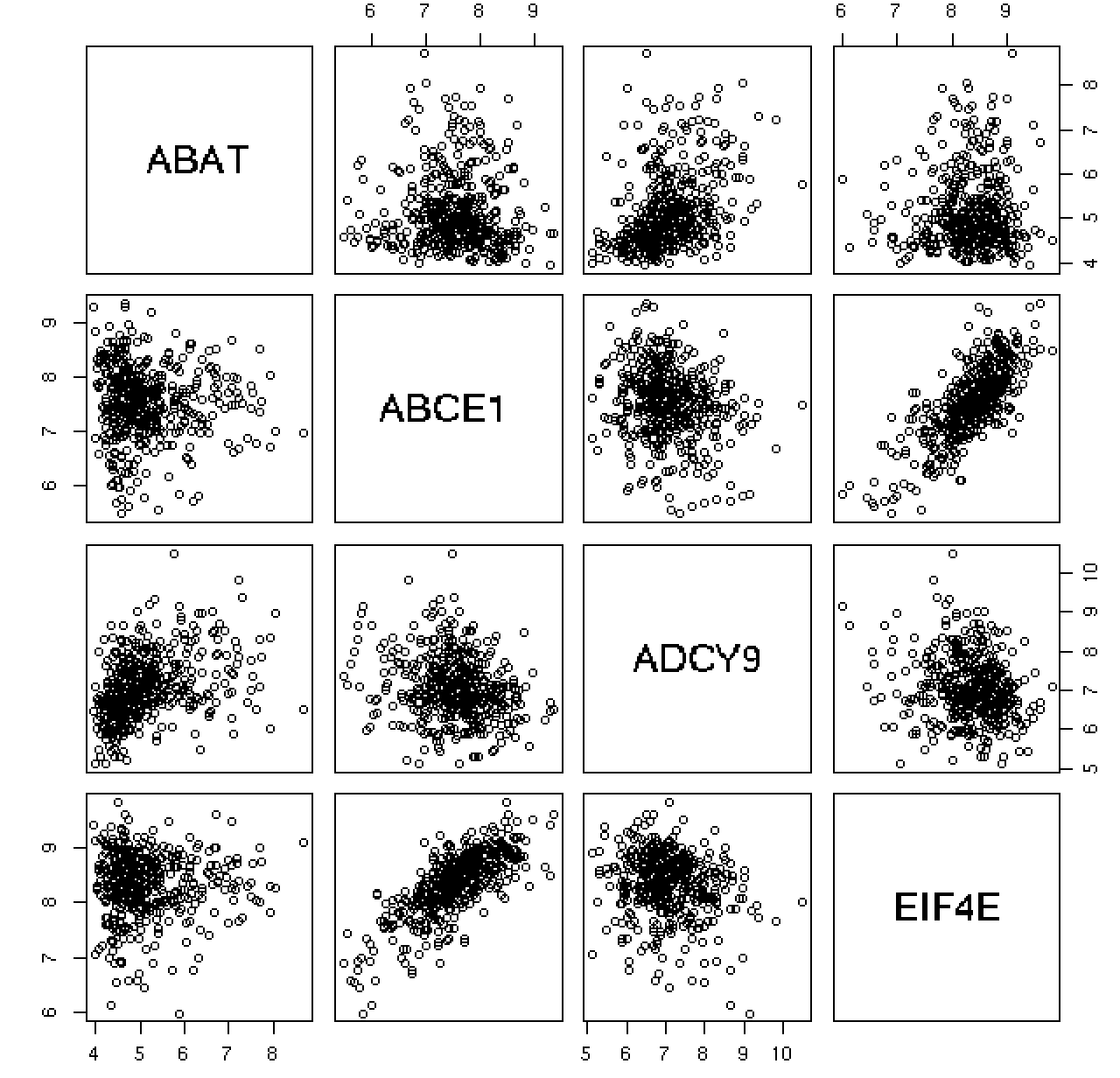
![pair_img]()
위의 사진이 산점도 행렬의 예시이다. (검은 부분은 검은색 원이 아니라 원이 많이 겹쳐버려서 까맣게 보이는 것이다.) 우선 대각성분들은 모두 자신과 자신의 조합이므로 의미가 없어서 해당 변수를 보여준다. 산점도 행렬들의 집합을 보면 유의미한 상관관계를 갖고 있는 변수조합은 (ABCE1, EIF4E)와 (EIF4E, ABCE1)임을 확인할 수 있다.
iris data
- iris Data
1 2 3 4 5 6 7
ind = c(2,8,12,200) pairs(expr_dat[,ind]) pairs(expr_dat[,ind], "Expression Data", pch = 21, bg = c("red","blue")[gr_ind]) dev.off() iris x11() pairs(iris[1:4], pch=c(0, 3, 4)[as.numeric(iris$Species)])
위에서 말했듯이 산점도 그래프는 머신러닝에 사용되는 경우가 많다. iris라는 데이터셋을 사용해서 판별분석을 연습할 수 있다. iris데이터에는 3가지의 아이리스 종류가 존재하는데, sepal과 petal의 정보로 구분을 할 수 있다. 그러기 위해서 우선 학습을 위해 어떤 변수 조합이 유의미한 지를 확인해볼 필요가 있다. 이는 선형회귀분석을 위해서 필요하기도 하다.
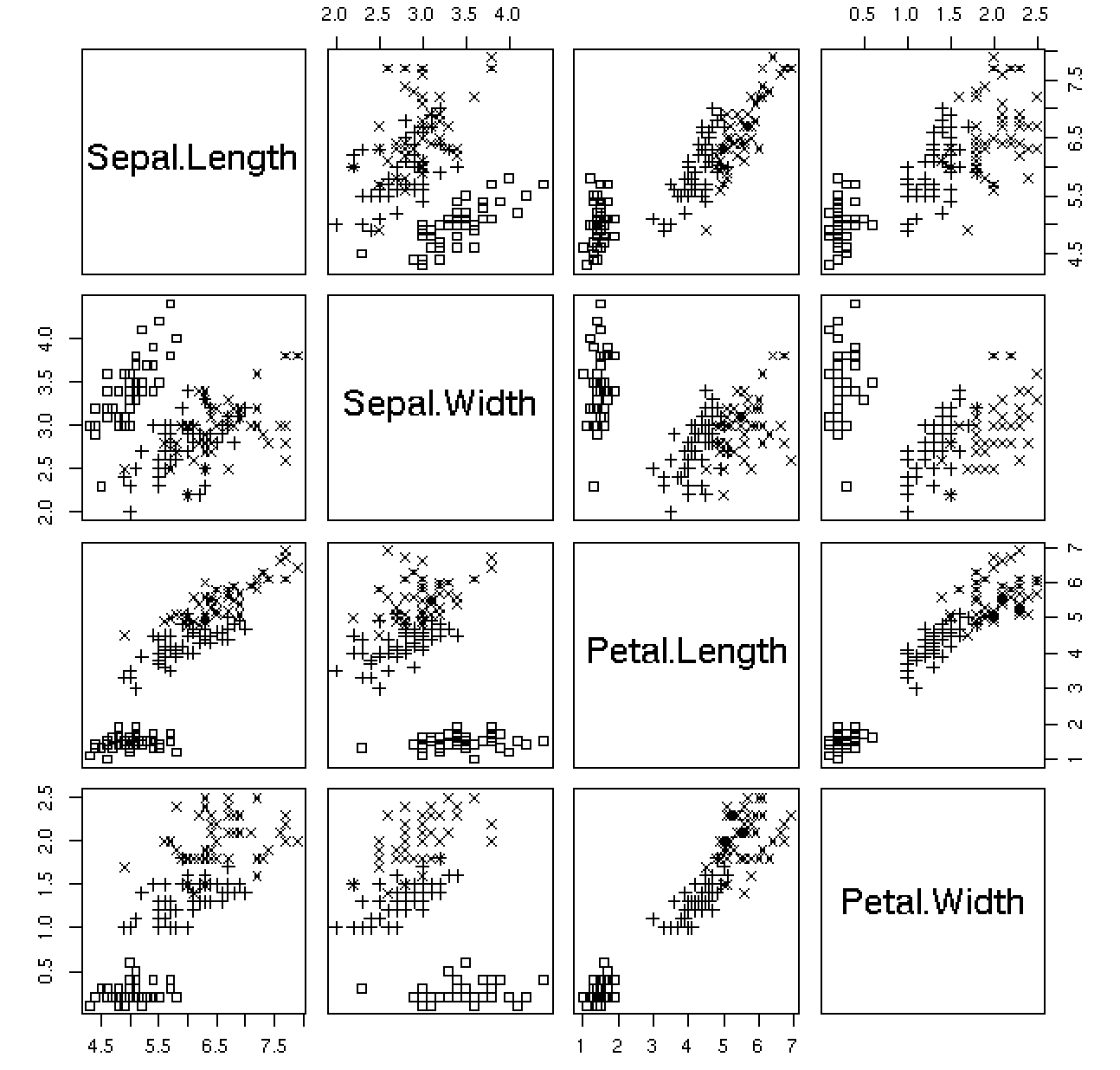
![iris]()
나름 의미가 있어보이는 데이터 셋은 (1,3), (2,4), (4,3), (3,4) 정도이다. (2,4)는 선형의 데이터도 아닌데 왜 의미가 있죠? 라고 묻는 사람들이 있을 수 있는데, 이 과정을 하는 이유는 구분 을 위해서이다. (2,4)의 데이터셋은 종별로 구분이 정확하게 잘 이뤄지고 있는 편이므로 판별분석에서는 충분히 가치가 있다.
위치의 측도
- 위치의 측도
- 평균 (mean, 산술평균)
일반적으로 평균이라고 말하는 값이다.
특이값(outlier)의 영향을 크게 받는다. 사용함수 :mean(vector, na.rm = T or F)- 중위수 (median, 중앙값)
데이터의 순위에 관한 정보만을 이용한다.
데이터셋 중앙부분의 값을 기록하는 것이기 때문에 특이값(outlier)의 영향을 덜받는다. 이를 통계학에서는 robust라고 한다.
사용함수 :median(vector)- 최빈값 (mode) 데이터셋에서 가장 빈도가 높은 값이다. R에는 따로 정해져 있지는 않아서 정의를 해야한다.
1 2 3 4 5 6 7 8
x = c(1,2,3,1,2,5,5,3,3,3,2) tb_x = table(x); tb_x as.numeric(names(tb_x)[which.max(tb_x)]) Mode = function(vec) { tb = table(vec) return(as.numeric(names(tb)[which.max(tb)])) } Mode(x)
- 분위수 (quantile) 특정 퍼센티지에 위치한 값을 말한다. 사용함수는
quantile()이다.
quantile(data_set, percentage, type)의 형식으로 파라미터를 적어준다. type은 특정 방법론을 대표하는데, 일반적으로 따로 기입하지 않는 경우도 많다.
사용함수 :quantile(data_set, percentage, type)
산포의 측도
- 산포의 측도
- 표본분산 (sample variance)
표본을 뽑아서 분산을 계산한다.
모분산 : $\sigma^2 = Var(X) = E((X-\mu)^2)$
모표준편차 : $\sigma = \sqrt{Var(X)}$
사용함수 :var(vector), sd(vector)- 변동계수 (coefficient of variation, 변이계수) $CV = \frac{s}{\overline x}\times 100(\%) $
자료의 측정단위에 의존하지 않는 상대적 산포의 측도이다.
측정단위가 다르거나 평균에 큰 차이가 있는 자료들의 산포를 비교할 때 사용한다.
사용함수 : 없음
왜도와 첨도 (skewness and excess kurtosis)
- 왜도와 첨도
- 왜도 (skewness)
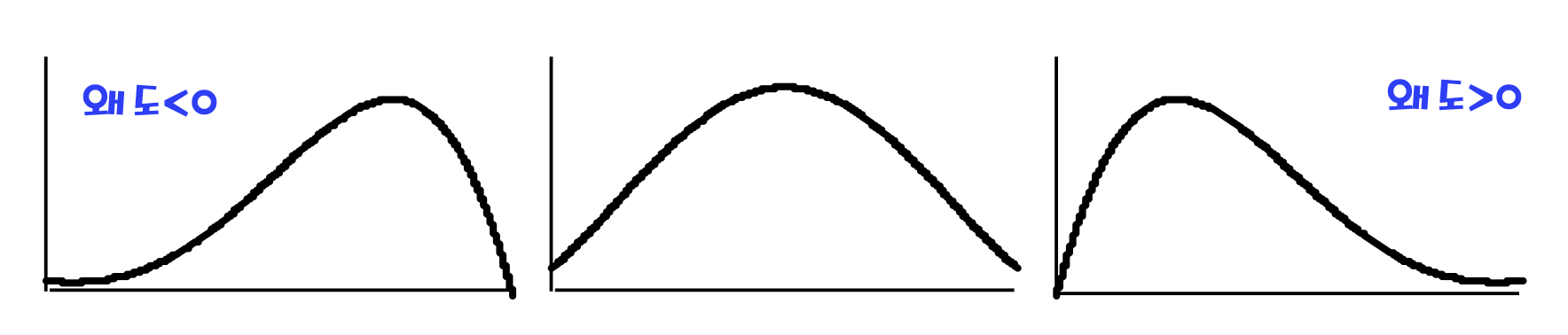
![skew]()
왜도는 비대칭의 정도를 보여준다. 일반적으로 0보다 큰 지 작은지를 확인하는데,
왜도가 0보다 작으면 우측으로 데이터가 치우친 것이고 왜도가 0보다 크면 좌측으로 데이터가 치우친 것이다. - 첨도 (excess kurtosis)
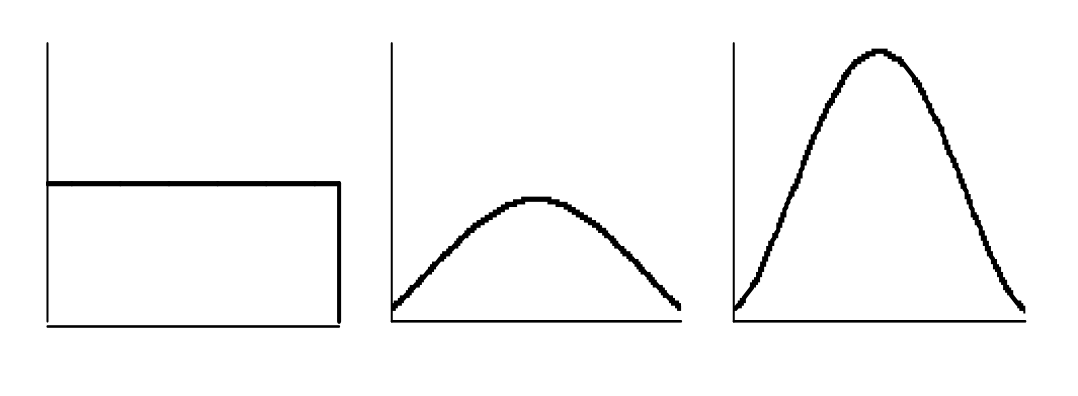
![kurtosis]()
그래프가 얼마나 뾰족한 형태를 가지는 지 알 수 있다.
\(\begin{cases} <3 : \text{flat (left distribution)} \newline =3 : \text{Normal distribution} \newline \text{> }3 : \text{steep (right distribution)} \end{cases}\)
사용함수 : moment package 내부에skewness(vector), kurtosis(vector)
- 왜도 (skewness)
데이터 요약 (summary)
- 데이터 요약 (summary)
1 2 3 4 5
x <- rnorm(100) summary(x) y <- c('red', 'blue', 'red','white') summary(y) f.y <- factor(y); summary(f.y)
말 그래도 데이터들의 정보를 요약해준다. 첫번째 데이터는 최대 최소, 4분위수들을 제공해준다.
만약 두번째 처럼 벡터요소가 들어가면 벡터의 정보가 반환된다. 그래서 벡터의 factor type적 요소로 제공을 해주면 자세한 해당 벡터의 정보를 반환해준다.
교차표 or 분할표 (cross table or contingency table)
- 교차표 or 분할표
1 2 3 4
table(mtcars$cyl) table(mtcars$am) table(mtcars$cyl, mtcars$am) table(mtcars$cyl, mtcars$am, mtcars$gear)
table 함수에 특정 변수를 넣으면 해당 변수들로 분할표를 만들어준다. 데이터 변수를 1개만 넣으면 해당 변수의 도수분포표를 보여주고 2개를 넣으면 2차원 분할표를 보여준다. 변수의 조합으로 나오는 값들을 보여준다.
변수를 3개 넣으면 3차원 분할표를 보여주는데, 3차원 큐브 형식의 데이터를 보여주는 것이 아니라 2차원 분할표에서 끝값만 변경해서 보여준다.
공분산 및 상관계수 (Covariance and Correlation)
- 공분산 (Covariance)
1 2 3
cov(expr_dat[,1], expr_dat[,5]) cov(expr_dat[,c(1,5,8)]) var(expr_dat[,1])
\(\sigma_{xy} = \mathrm{Cov}(X,Y) = E[(X-E(X))(T - E(Y))]\)
두 변수 사이의 연관성의 방향을 알 수 있지만 크기의 비교는 어렵다.
공분산을 통해 두 변수의 음의 상관성, 양의 상관성을 확인할 수 있다.- 표본 공분산 \(s_{xy}=\frac{1}{n-1}\sum_{i=1}^{n}(x_i - \overline x)(y_i - \overline y)\)
- 상관계수 (Correlation)
1
cor(expr_dat[,1], expr_dat[,5])
\(\rho = \mathrm{Corr}(X,Y)=\frac{\sigma_{XY}}{\sigma_X\sigma_Y}\)
공분산을 각각의 표준편차로 나눈 값으로 상대적인 크기 비교가 가능하다.

Comments powered by Disqus.