Binary Tree (이진 트리)

이진트리 개념

이진트리는 우리가 이전에 배운 트리의 특수한 형태이다. 일반 트리가 자식 수에 제한이 없다면, 이진트리는 1부모에 최대 2개의 자식 노드가 존재한다.
보통 왼쪽 노드, 오른쪽 노드라고 부르며 왼쪽 노드가 오른쪽 노드보다 우선하는 성질을 가진다. 일반 트리에서 설명하지 않았지만 트리는 자식간에 순서가 있는 ordered pair이다.
이진트리의 쓰임새는 아래와 같은 것들이 있다.

수식의 표현 트리
수식의 계산 트리
결정트리

우선 결정트리부터 설명해보면 internal node는 결정요소를 갖고있고 external node는 해당 결정요소에대한 결정 값들을 갖고있다.
후에 서술할 중위순회를 이용하면 수식을 표현할 수 있다.

완전 이진트리의 성질

완전 이진트리는 이진트리에서의 모든 internal node의 자식이 2개로 꽉 차있는 상태의 이진트리를 말한다. 이런 이진트리에서는 특별한 수식적 성질들이 있다. 우선 설명을 하기 전에 간단한 기호의 규칙들을 정해보겠다.

n : 노드의 개수
e : 리프 노드의 개수 (number of external nodes)
i : internal nodes의 개수
h : 높이

위와 같이 정하고 완전 이진트리의 성질을 이야기해보자.

$ e = i + 1$ 리프노드의 수는 내부노드 + 1이다. 왜 그럴까?
모든 노드는 2개의 자식을 갖고 있다. 그래서 만약 여기서만 internal node가 n개면 총 2n개의 자식이 존재한다. (어떤 부모는 다른 부모의 자식일 수 있다.)
이때, 모든 루트노드를 제외한 모든 노드는 부모를 갖고 있다. 결국 n-1개의 노드가 부모를 갖고 있다.
그 뜻은 다른 말로 말하면 n-1개의 부모 노드는 적어도 n-1개의 자식을 확실하게 확보하고 있다.
그니까 이게 뭔 말이냐면, 자식이 존재하는 노드를 internal node인데 root노드는 부모노드가 없는 노드이다. internal node가 있다는 것은 이 노드는 누군가의 자식이라는 거다. 즉 전체 internal node수인 n개에서 root노드를 제외하곤 부모와 연결하는 n-1개의 연결을 필요로 하게된다.
최종적으로 반드시 사용해야하는 n-1개를 2n개에서 빼면 n+1개의 자리가 남는다. 이 n+1개는 반드시 external nodes가 되게 된다.
$ n = 2e - 1$ 전체 노드의 개수는 n개인데, $ n = i + e$ 의 성질을 갖는다. 1번 식에 해당 식을 정리해서 대입하고 다시 정리하면 2번 식이 나오게된다.
$ h \leq i$
트리의 높이는 internal node의 개수보다 작거나 같다. 이건 생각보다 생각하기 간단하다. 모든 노드가 한 줄로 쭉 연결된 상태라고하면, h와 i의 값이 같다. h는 자식이 하나 뻗을 때마다 1개씩 증가하기 때문이다.
$ h \leq (n - 1) / 2$
이 식은 3번과 1,2번 식을 정리하면된다.
$n = 2e - 1 = 2(i + 1) - 1 = 2i + 1 \\ \therefore \; i = (n - 1) / 2$
위의 계산과정을 3번에 대입하면 4번이 나온다.
$ e \leq 2^h$
이건 3번의 증명과 좀 반대로 생각하고 좌우가 균형을 이후는 완전 이진트리를 그리면 된다.
$ h \geq log_{2}e, \;\;h\geq log_{2}(n+1) - 1$
5번 식을 양변로그를 취하고 4번의 식을 합쳐주면 두 식이 나오게 된다.

이진트리 순회

이진트리도 일종의 트리이다. 결국 순회가 존재하는데, 앞서 말했던 전위, 후위순회는 동일하게 진행되고 이진트리에만 있는 특수한 순회가 있다. 바로 중위순회 (inorder traversal)이다.
중위순회는 전위, 후위순회와 조금 다른 특징이라면 다음 자식을 가기 전에 자신을 거치고 간다는 점이다. 즉, 왼쪽->나->오른쪽의 탐색순서를 거친다는 의미이다.

Algorithm inOrder(v)
  if !v.isExternal()
    inOrder(v.left())

  visit(v)

  if !v.isExternal()
    inOrder(v.right())

중위순회는 다음과 같이 탐색한다.

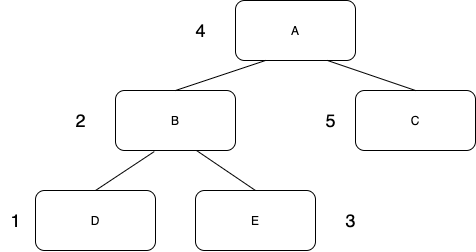
inorder

사실 가만히 놓고 보면 모든 순회는 재귀함수 구현이 주를 이룬다.

수식 출력

중위순회를 사용하면 수식 출력이 가능하다.

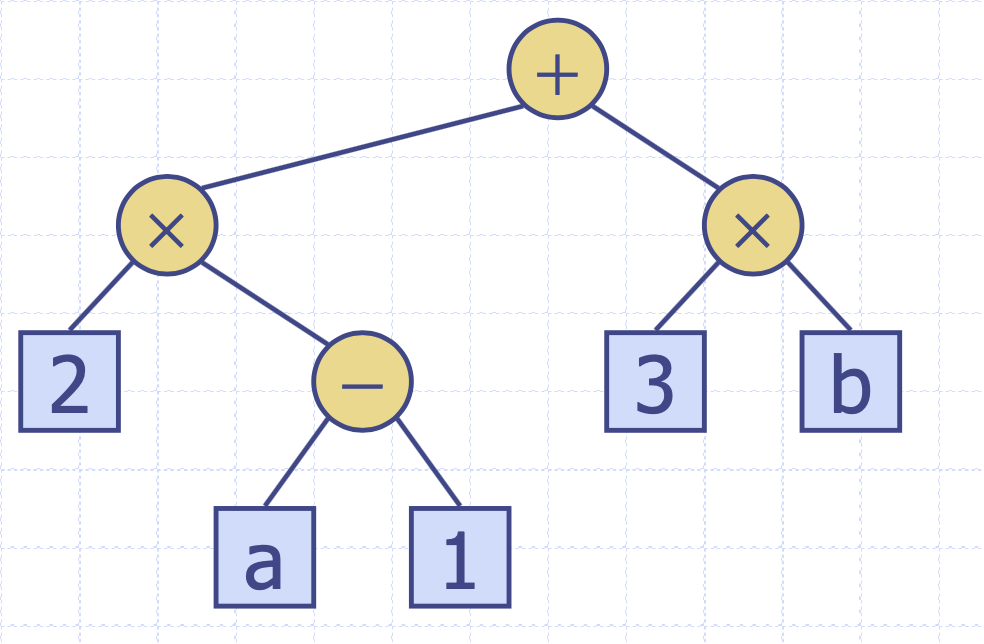
arith
위의 수식을 중위순회로 원래 수식으로 표현할 수 있다.

Algorithm inOrder(v)
  if !v.isExternal()
    print('(')
    inOrder(v.left())

  print(v.element())

  if !v.isExternal()
    inOrder(v.right())
    print(')')

이렇게 코드를 작성하면 숫자 -> 수식의 형태로 탐색하게된다. 출력결과는 잘 생각해보길… 코드를 따라가면서 해석하는 것도 중요하다.

Tree implementation (트리 구현)

Node prototype

  
#include <vector>
using namespace std;

class Node {
private:
  Node* parent;
  int data;
  vector<Node*> children;

public:
  Node() {
    parent = NULL;
    data = NULL;
  }

  Node(int d) {
    parent = NULL;
    data = d;
  }

  void insetChild(Node* c) {
    this->children.push_back(c);
    return;
  }

  void deleteChild(Node* c) {
    for (int i = 0; i < children.size(); i++) {
      if (children[i] == c) {
        this->children.erase(this->children.begin() + i);
        break;
      }
    }
  }

  ~Node() {}

  friend class Tree;
};

이건 트리에 필요한 노드의 클래스이다. 트리에 들어가는 노드는 부모를 가리키는 노드 포인터와 자식 노드들을 저장하는 노드포인터 벡터가 존재한다. 트리에서 좀 더 쉽게 사용할 수 있는 insert와 delete가 있다.

Tree prototype

  
#include <vector>
using namespace std;

class Node {...};

class Tree {
private:
  int tmp = 0;
  int heiht = 0;
  Node* root;
  vector<Node*> node_list;

public:
  Tree() {
    root = NULL;
  }

  Tree(int d) {
    root = new Node(d);
  }

  Node* getRoot();
  void insert(int p, int c);
  void delNode(int data);
  int getHeight();
  void printChild(int data);
  void countDepth(int data);
  void preorder(Node* n);
  void postorder(Node* n);
  Node* findNode(int data);
}

생성자는 2개를 만들었다. 일반적으로 생성하는 기본생성자는 root node가 NULL값이고 특정 데이터를 갖는 노드를 루트로 하려면 두번째 생성자를 해주면된다. 멤버변수에 대해서 간단히 설명하자면, root는 말 그대로 루트노드를 말한다, node_list는 현재 트리에 저장된 노드를 저장하는 벡터이다. 이 트리의 저장형태를 간단히 표시하면 아래와 같다.

node
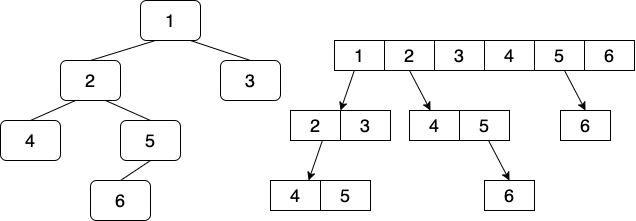
우측의 배열이 좌측의 트리에 있는 node_list에 저장된 값들이고 해당 노드들의 children을 보여준다.

getroot, getheight function

  
Node* getRoot() {
  return root;
}

int getHeight() {
  return height;
}

두 함수는 간단하다. 그냥 요구하는 걸 반환해주면 된다.

insert function

  
void insert(int p, int c) {
  bool exist = false; // 부모노드가 있는 지 확인한다.

  for(int i = 0; i < node_list.size(); i++) {
    if(node_list[i]->data == p) {
      exist = true;

      Node* v = new Node(c);

      node_list[i].push_back(v);
      node_list[i]->insetChild(v);
      v->parent = node_list[i];
      break;
    }
  }

  if(!exist)
    cout << -1 << "\n";

}

exist변수는 자식을 추가하려고하는 부모노드의 존재를 확인하는 플래그 변수이다. 기본적으로 Node 클래스에 만들어 둔 insertChild 함수를 활용한다.
부모노드의 역할을 하는 노드에 있는 자식노드 리스트 벡터에 저장을 하는 원리이다.

현재 있는 노드리스트에서 찾고자 하는 부모노드를 탐색한다.
찾은 노드의 자식 노드리스트 벡터에 새로운 노드인 자식노드를 넣어준다.
새롭게 만든 자식노드의 부모포인터를 현재 노드로 지정해준다.

delete function

  
void delNode(int data) {
  bool exist = false;

  for(int i = 0; i < node_list.size(); i++) {
    if (node_list[i]->data == data) {
      exist = true;
      Node* p = node_list[i]->parent;

      for(int j = 0; j < node_list[i]->children.size(); j++) {
        // 삭제하고자하는 노드의 자식을 모두 삭제 노드의 부모로 연결해준다.
        node_list[i]->children[j]->parent = p;
        p->children.push_back(node_list[i]->children[j]);
      }

      p->deleteChild(node_list[i]);
      delete node_list[i];

      break;
    }
  }

  if (!exist)
  cout << -1 << "\n";
}

실제로 문제풀이 때 사용할 일이 없어서 구현은 안 했지만 이론상 설명을 하기위해서 직접 구현을 했다. 내가 배운 특정 노드 제거 방법은 제거하고자하는 노드의 자식들을 제거하는 노드의 부모 노드로 옮기는 과정으로 진행한다.

삭제하고자하는 노드가 있는지 확인한다.
노드가 있다면 해당 노드의 자식노드리스트 크기만큼 돌려준다.
옮긴 부모 노드의 자식 노드리스트 벡터에 해당 자식들을 추가해준다.
모든 작업이 끝나면 해당 노드를 부모 노드에서 제거해준다.
최종적으로 원하는 노드를 제거한다.

count depth function

  
int countDepth(int data) {
  int d = 0; // return value;
  bool exist = true;

  for (int i = 0; i < node_list.size(); i++) {
      if (node_list[i]->data == data) {
        exist = false;
        // depth 계산 시작 노드 탐색 완료 거꾸로 올라간다

        for (Node* curr = node_list[i]; curr->parent != NULL; curr = curr->parent) {
            d++;
        }
      }
  }

  if(exist)
    return -1;

  return d;
}

노드의 깊이는 현재 노드가 루트 노드를 만나러 올라갈 때까지 카운팅을 올려주면 된다.
노드를 찾고 역으로 타고 올라가면 된다.

노드리스트에서 찾고자하는 노드를 탐색한다.
노드를 발견하면 현재 노드를 기준으로 계속해서 부모노드로 올라간다.
부모노드가 NULL인 루트노드를 발견하면 카운트를 멈춘다.

print child function

  
void printChild(int data) {
  bool exist = false;

  for(int i = 0; i < node_list.size(); i++) {
    if (node_list[i]->data == data) {
      exist = true;
      int s = node_list[i]->children.size();

      if (s == 0){
        cout << 0 << "\n";
      }else{
        for(int j = 0; j < s; j++) {
          cout << node_list[i]->children[j]->data << " ";
        }

        cout << "\n";
      }
    }
    break;
  }

  if(exist)
    cout << -1 << "\n";
}

특정 노드의 자식 노드를 출력하는 함수이다. 코드는 길어보이나 아이디어는 간단하다.
필요로하는 노드를 node_list에서 찾고 그 노드의 자식 노드 벡터를 다 출력해주면 되는 것이다. 문제에서 요구하는 사항이 0이나 -1을 출력하는 것이 있어서 이것저것 많이 있게 되었다.
하지만 프로그래밍은 원래 예외처리가 중요하므로 해줄 필요가 충분히 있다.

find node function

  
Node* findNode(int data) {
  for(int i = 0; i < node_list.size(); i++) {
    if (node_list[i]->data == data) {
      return node_list[i];
    }
  }

  return NULL;
}

특정 노드를 탐색하는 함수이다. 앞서서 진행한 insert, delete, print등에 활용한 기반 함수를 활용하면 된다. 반복문으로 node_list에서 탐색하면 된다.

preorder function

  
void preorder(Node* node) {
  cout << node->data << " ";

  if(node->children.size() != 0) {
    tmp++; // 자식이 있으므로 깊이 연산가능하다.

    for(int i = 0; i < node->children.size(); i++) {
      Node* child = node->children[i];
      preorder(child);
    }

    if(tmp > height)
      height = tmp;

    tmp--;
  }
}

전위순회 출력결과를 실행해주는 함수이다. 전위순회를 하는 동시에 전체 트리의 높이를 계산해주는 기능이 들어가있다.

자신 노드의 값을 출력해준다.
자신에게 자식노드가 있다면 이제 전위순회를 시행한다.
각자 노드의 깊이를 계산해주는 임시 변수 tmp를 늘려준다.
자식 수만큼 반복문을 돌리며 자식에 대해서 전위순회를 재귀함수로 시행해준다.
만약 자식이 없는 리프노드에 도달할경우 다시 재귀 실행 이전으로 돌아오게 된다.
모든 반복문이 종료되고 높이를 갱신해준다.
자식이 있는 노드의 깊이 계산이 끝났으므로 재귀 실행 이전으로 돌아가기전에 높이를 줄여준다.

if문 안에 있는 tmp를 늘리고 줄이는 순서의 위치는 향후에 그래프 탐색을 할 때 쓰는 DFS에서 사이클 내부에 존재하는 노드 개수 계산과도 큰 관련이 있으므로 기억해두면 좋다.

postorder function

  
void postorder(Node* node) {
  if(node->children.size() != 0) {
    for (int i = 0; i < node->children.size(); i++) {
      Node* child = node->children[i];
      postorder(child);
    }
  }

  cout << node->data << " ";
}

후위순회는 전위순회에서 출력 순서만 맨 뒤로 옮겨주면 된다. 원리는 전위순회와 동일하다.

중위순회에 대한 내용은 티스토리 블로그 트리 설명에 올려질 예정이다.

[Data Structure] Binary Tree (이진트리) & Tree 구현